Zadanie nr 4726522
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 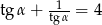 , oblicz
, oblicz 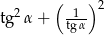 .
.
Rozwiązanie
Sposób I
Podnosimy daną równość stronami do kwadratu.
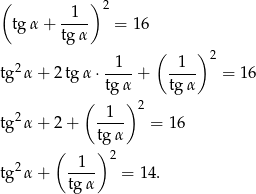
Sposób II
Przekształćmy daną równość
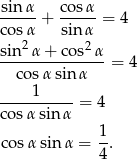
Teraz przekształćmy wyrażenie, które mamy obliczyć
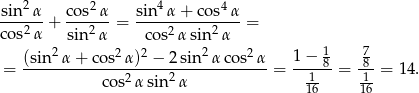
Sposób III
Podstawmy 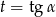 . Mamy wtedy
. Mamy wtedy
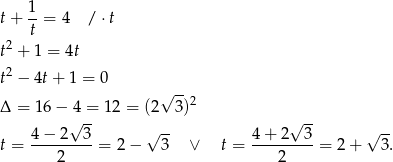
Mamy więc
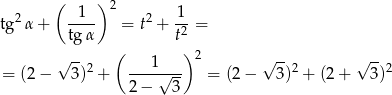
lub
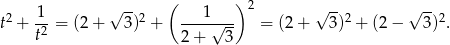
W każdym z przypadków mamy ten sam wynik
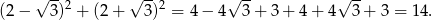
Odpowiedź: 14

