/Szkoła średnia/Funkcje/Trygonometryczna

Zadanie nr 5624325

Dodaj do ulubionych
Dodaj do rozwiązanych

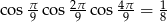Wykaż, że π- 2π- 4π- 1 cos 9 co s 9 cos 9 = 8 .

Rozwiązanie

Sposób I

Ponieważ drugi i trzeci kąt są dwukrotnością kąta poprzedniego, domnażamy równość tak, aby uzyskać wzór na 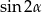sin 2α .

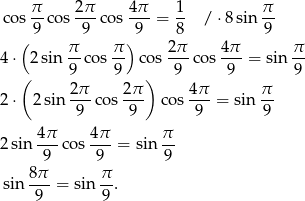
co s π cos 2-π cos 4π-= 1- / ⋅8sin π- 9 9 9 8 9 ( π- π-) 2π- 4π- π- 4 ⋅ 2 sin 9 cos 9 cos 9 co s 9 = sin 9 ( 2π 2π ) 4π π 2 ⋅ 2sin ---cos --- cos --- = sin -- 9 9 9 9 4π- 4-π π- 2 sin 9 cos 9 = sin 9 8π π sin --- = sin --. 9 9

Otrzymana równość jest oczywiście spełniona (bo 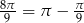8π- π- 9 = π − 9 ), a przekształcaliśmy ją w sposób równoważny, więc wyjściowa równość też musiała być spełniona.

Sposób II

Tym razem będziemy przekształcać równość kilkukrotnie korzystając ze wzoru na cosinus sumy

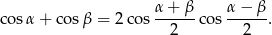
α+ β α − β co sα + cos β = 2 cos ------cos------. 2 2

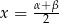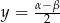Ponieważ będziemy chcieli używać tego wzoru do zamiany iloczynu na sumę, wygodnie jest podstawić w tym wzorze α+β x = -2-- i y = α−β- 2 . Przy takich oznaczeniach wzór ten przyjmuje postać

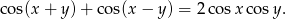
co s(x+ y)+ cos(x − y) = 2 cosx cos y.

Przekształcamy daną równość w sposób równoważny.

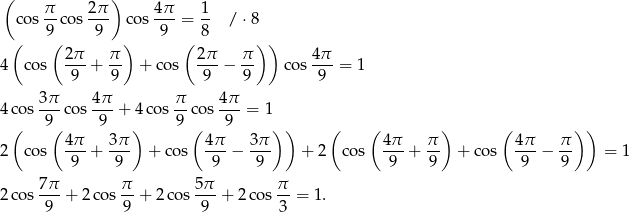
( π 2π ) 4π 1 cos --cos --- cos --- = -- / ⋅8 ( 9( 9 ) 9 ( 8 )) 2π- π- 2π- π- 4-π 4 cos 9 + 9 + cos 9 − 9 cos 9 = 1 4co s 3π cos 4-π + 4 cos π-cos 4π-= 1 ( 9( 9 ) 9 ( 9 ) ) ( ( ) ( ) ) 4π 3π 4π 3π 4π π 4π π 2 cos 9--+ -9- + co s -9-− -9- + 2 cos -9- + 9- + cos -9- − 9- = 1 2co s 7π + 2 cos π + 2 cos 5-π + 2 cos π-= 1. 9 9 9 3

Ponieważ 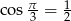cos π-= 1 3 2 , powyższa równość jest równoważna równości

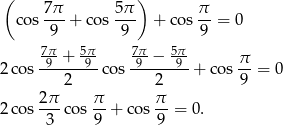
( 7π 5π ) π cos ---+ co s--- + cos --= 0 9 9 9 7π-+ 5π-- 7π-− 5π- π 2cos -9----9-c os-9-----9 + co s-- = 0 2 2 9 2cos 2π-co s π + cos π-= 0. 3 9 9

Powyższa równość jest oczywiście spełniona (bo 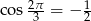cos 2π3-= − 12 ), więc wyjściowa równość też musiała być spełniona.

Wersja PDF