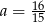/Szkoła średnia/Funkcje/Trygonometryczna

Zadanie nr 6356908

Dodaj do ulubionych
Dodaj do rozwiązanych

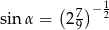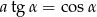Wiedząc, że α jest miarą kąta ostrego i ( )− 1 sin α = 2 79 2 , wyznacz liczbę a , dla której atgα = cosα .

Rozwiązanie

Mamy

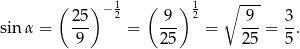
( ) −1 ( ) 1 ∘ --- sin α = 25- 2 = -9- 2 = 9--= 3-. 9 25 25 5

Sposób I

Zobaczmy co mamy policzyć

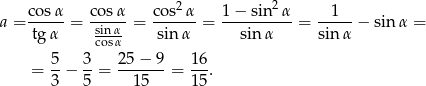
2 2 a = cosα-= cos-α = cos-α-= 1-−-sin-α- = --1-- − sinα = tg α sinα- sin α sin α sin α cosα = 5-− 3-= 25-−-9-= 16. 3 5 15 15

Zauważmy, że nie była w tych rachunkach potrzebna informacja o tym, że α jest kątem ostrym.

Sposób II

Zamiast przekształcać dane wyrażenie, możemy policzyć 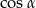cos α i tg α .

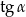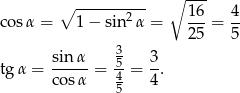
∘ ---------- ∘ --- cosα = 1 − sin2α = 16-= 4- 25 5 sinα 3 3 tg α = -----= 54-= --. cosα 5 4

Mamy zatem

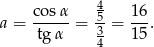
4 cos-α -5 1-6 a = tg α = 3 = 1 5. 4

Tutaj korzystaliśmy z tego, że α jest kątem ostrym przy wyborze znaku przy cosinusie.  
Odpowiedź: a = 1165

Wersja PDF