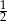Zadanie nr 7609534
Kąt  jest ostry i
jest ostry i 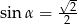 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 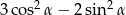 .
.
Rozwiązanie
Sposób I
Jeżeli 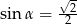 to
to 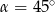 i
i 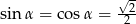 . Mamy zatem
. Mamy zatem
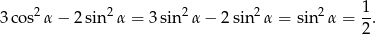
Sposób II
Na mocy jedynki trygonometrycznej mamy
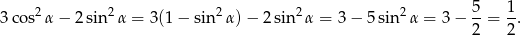
Odpowiedź: 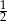
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Kąt  jest ostry i
jest ostry i 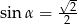 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 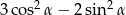 .
.
Sposób I
Jeżeli 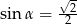 to
to 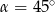 i
i 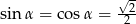 . Mamy zatem
. Mamy zatem
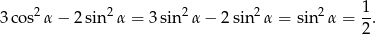
Sposób II
Na mocy jedynki trygonometrycznej mamy
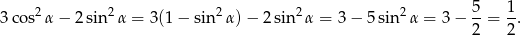
Odpowiedź: