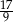/Szkoła średnia/Funkcje/Trygonometryczna

Zadanie nr 9294577

Dodaj do ulubionych
Dodaj do rozwiązanych

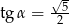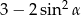Kąt α jest kątem ostrym i √5- tg α = 2 . Oblicz 2 3− 2 sin α .

Rozwiązanie

Sposób I

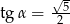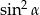Przekształćmy daną równość: √ - tg α = --5 2 tak, aby wyliczyć sin2 α .

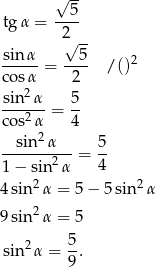
√ -- --5- tg α = 2 √ -- sin-α-= --5- /()2 cosα 2 sin 2α 5 ---2--= -- cos α 4 --sin2-α--- 5- 1− sin2 α = 4 2 2 4 sin α = 5− 5sin α 9 sin 2α = 5 sin 2α = 5. 9

Zatem

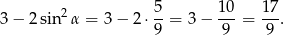
3− 2 sin2α = 3− 2⋅ 5-= 3 − 1-0 = 17-. 9 9 9

Sposób II

Narysujmy trójkąt prostokątny, w którym tanges ma wartość 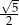√-5 2 .

PIC

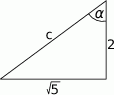
Obliczamy z twierdzenia Pitagorasa długość przeciwprostokątnej

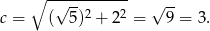
∘ ----------- √ --2 2 √ -- c = ( 5) + 2 = 9 = 3.

Zatem 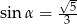√ - sin α = -35 oraz

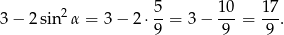
3− 2 sin2α = 3− 2⋅ 5-= 3 − 1-0 = 17-. 9 9 9

 
Odpowiedź: 179

Wersja PDF