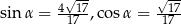/Szkoła średnia/Funkcje/Trygonometryczna

Zadanie nr 9660070

Dodaj do ulubionych
Dodaj do rozwiązanych

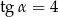Kąt α jest kątem ostrym i tg α = 4 . Wyznacz sinus i cosinus tego kąta.

Rozwiązanie

Sposób I

Szukane wartości wyznaczymy z układu równań

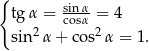
{ tg α = sinα = 4 cosα sin2α + co s2α = 1 .

Z pierwszego równania wyznaczamy 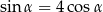sin α = 4 cos α i podstawiamy do drugiego równania

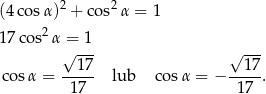
(4cos α)2 + cos2α = 1 2 17cos α = 1 √ --- √ --- cos α = --17- lub cos α = − --17-. 17 17

Ponieważ α jest kątem ostrym, więc zarówno sinus jak i cosinus mają wartości dodatnie. Zatem możemy odrzucić rozwiązanie ujemne. Stąd otrzymujemy, że

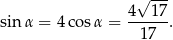
√ --- 4--17- sinα = 4co sα = 17 .

Sposób II

Narysujmy trójkąt prostokątny, w którym tanges ma wartość 4

PIC

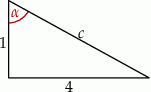
Obliczamy długość przeciwprostokątnej z twierdzenia Pitagorasa

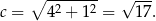
∘ ------- √ --- c = 42 + 12 = 17.

Teraz wystarczy tylko podstawić i obliczyć szukane wartości

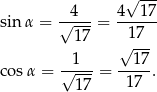
√ --- 4 4 1 7 sin α = √---- = ------ 1 7 √17-- -1--- --17- co sα = √ ---= 17 . 17

 
Odpowiedź: 4√ 17 √ 17 sin α = -17-,cosα = -17-

Wersja PDF