/Szkoła średnia/Funkcje - wykresy/Homografia/Przesunięcie wykresu

Zadanie nr 7306529

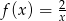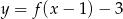Dana jest funkcja 2 f (x) = x . Narysuj wykres i wyznacz przedziały monotoniczności funkcji y = f(x − 1 )− 3 .

Wersja PDF

Rozwiązanie

Sposób I

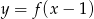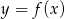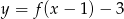Funkcja y = f(x − 1) powstaje z wykresu y = f(x) przez przesunięcie o jedną jednostkę w prawo. Jeżeli tak otrzymany wykres przesuniemy o 3 jednostki w dół, otrzymamy wykres y = f (x− 1)− 3 .

Teraz bez trudu rysujemy wykres.

PIC

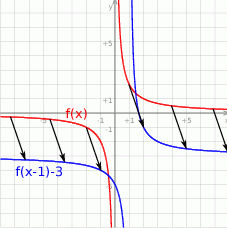
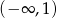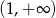Przedziały monotoniczności odczytujemy z wykresu: funkcja maleje na każdym z przedziałów (− ∞ ,1) i (1,+ ∞ ) (ale nie jest malejąca na sumie tych przedziałów!).

Sposób II

Korzystamy ze wzoru na przesunięcie funkcji 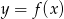y = f(x ) o wektor →v = [a,b] :

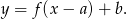
y = f(x − a) + b.

W naszej sytuacji, wykres funkcji 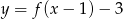y = f(x − 1 )− 3 powstaje z wykresu funkcji 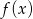f (x) przez przesunięcie o wektor [1,− 3] .

Dalej postępujemy jak w poprzednim sposobie.  
Odpowiedź: Malejąca na przedziałach 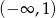(− ∞ ,1) i (1,+ ∞ )

Wersja PDF