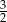Zadanie nr 9120378
Na rysunku przedstawiony jest wykres funkcji  określonej wzorem
określonej wzorem 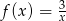 dla
dla 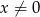 .
.
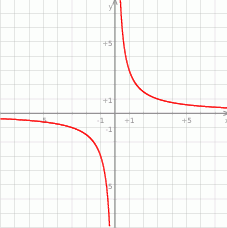
Wykres ten przesunięto o 2 jednostki w górę wzdłuż osi 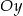 . Otrzymano w ten sposób wykres funkcji
. Otrzymano w ten sposób wykres funkcji 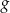 o wzorze
o wzorze 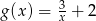 dla
dla 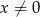 .
.
- Narysuj wykres funkcji
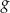 .
. - Oblicz największą wartość funkcji
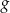 w przedziale
w przedziale 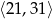 .
. - Podaj, o ile jednostek wzdłuż osi
 należy przesunąć wykres funkcji
należy przesunąć wykres funkcji 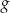 , aby otrzymać wykres funkcji przechodzący przez początek układu współrzędnych.
, aby otrzymać wykres funkcji przechodzący przez początek układu współrzędnych.
Rozwiązanie
- Tak jak to jest opisane w treści, trzeba wykres
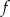 przesunąć o dwie jednostki w górę - rysunek.
przesunąć o dwie jednostki w górę - rysunek. 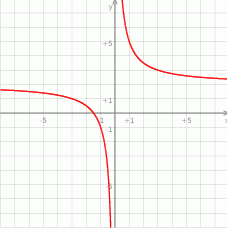
- Z narysowanego wykresu jest jasne, że na przedziale
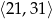 funkcja
funkcja 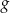 jest malejąca. Zatem największa wartość na tym przedziale to
jest malejąca. Zatem największa wartość na tym przedziale to 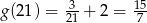 .
.
Odpowiedź: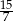
- Z rysunku widać, że kluczowe jest znalezienie punktu, w którym wykres przecina oś
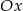 . Musimy w tym celu rozwiązać równanie
. Musimy w tym celu rozwiązać równanie 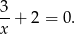
Łatwo wyliczyć, że
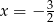 . Zatem aby wykres
. Zatem aby wykres 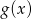 miał miejsce zerowe w punkcie
miał miejsce zerowe w punkcie 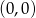 musimy go przesunąć o
musimy go przesunąć o  jednostki w prawo.
jednostki w prawo.
Odpowiedź: