Zadanie nr 4267284
Wyznacz wszystkie wartości parametru 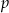 , dla których równanie
, dla których równanie 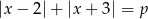 ma dokładnie dwa rozwiązania.
ma dokładnie dwa rozwiązania.
Rozwiązanie
Sposób I
Mamy do rozpatrzenia 3 przypadki.
Jeżeli 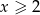 to mamy równanie
to mamy równanie
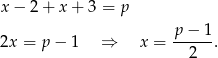
Sprawdźmy jeszcze kiedy 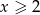 .
.
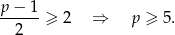
Jeżeli 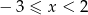 to mamy
to mamy
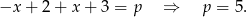
Jeżeli 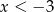 to mamy równanie
to mamy równanie
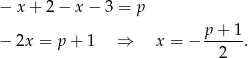
Sprawdźmy kiedy 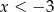
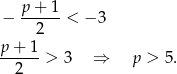
Widać z powyższych rachunków, że dokładnie dwa pierwiastki będą dla 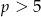 (dla
(dla 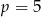 jest nieskończenie wiele rozwiązań).
jest nieskończenie wiele rozwiązań).
Sposób II
Tym razem narysujemy wykres lewej strony. Aby to zrobić, zapiszmy lewą stronę bez wartości bezwzględnej.
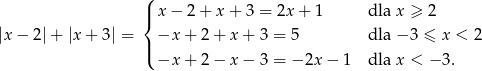
Rysujemy teraz wykres i bez trudu odczytujemy, że przecina się on z prostą 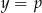 w dokładnie dwóch punktach dla
w dokładnie dwóch punktach dla 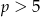 .
.
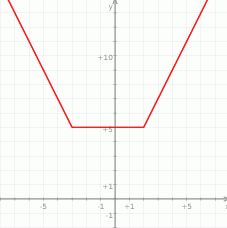
Odpowiedź: