/Szkoła średnia/Równania/Z wartością bezwględną/Liniowe/Z parametrem

Zadanie nr 4750379

Wyznacz te wartości parametru 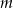m , dla których równanie 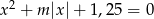2 x + m |x|+ 1,25 = 0 ma cztery rozwiązania.

Wersja PDF

Rozwiązanie

Równanie możemy zapisać w postaci

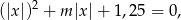
2 (|x|) + m |x |+ 1,25 = 0,

czyli

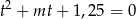
2 t + mt + 1,25 = 0

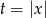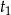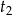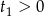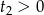dla t = |x | . Kiedy równanie będzie miało cztery rozwiązania? – aby tak było muszą być dwa pierwiastki t1 i t2 powyższego równania oraz każdy z tych pierwiastków musi dawać dwie wartości x . Oznacza to, że musimy mieć t > 0 1 , t > 0 2 . Zauważmy, że wtedy automatycznie pierwiastki pochodzące od 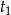t1 są różne od pierwiastków pochodzących od t2 .

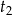Zacznijmy od sprawdzenia kiedy równanie ma dwa pierwiastki

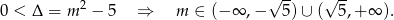
√ -- √ -- 0 < Δ = m 2 − 5 ⇒ m ∈ (− ∞ ,− 5)∪ ( 5,+ ∞ ).

Sprawdźmy kiedy pierwiastki równania są dodatnie. Tak będzie gdy ich suma i iloczyn są dodatnie. Na mocy wzorów Viète’a mamy

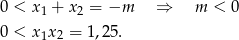
0 < x + x = −m ⇒ m < 0 1 2 0 < x1x2 = 1 ,25.

 
Odpowiedź: √ -- m ∈ (− ∞ ,− 5)

Wersja PDF