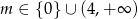/Szkoła średnia/Równania/Z wartością bezwględną/Liniowe/Z parametrem

Zadanie nr 5853188

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie wartości parametru 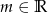m ∈ R , dla których równanie 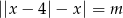||x− 4|− x | = m ma tylko jedno rozwiązanie.

Rozwiązanie

Zauważmy, że

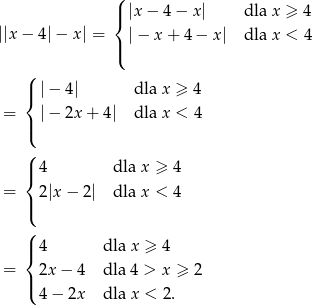
( |{ |x − 4 − x| dla x ≥ 4 ||x − 4|− x| = |− x+ 4− x| dla x < 4 |( ( | |− 4| dla x ≥ 4 { = | |− 2x+ 4| dla x < 4 ( ( |{ 4 dla x ≥ 4 = 2|x − 2| dla x < 4 |( ( |{ 4 dla x ≥ 4 = 2x − 4 dla 4 > x ≥ 2 |( 4 − 2x dla x < 2.

Teraz bez trudu szkicujemy wykres lewej strony równania.

PIC

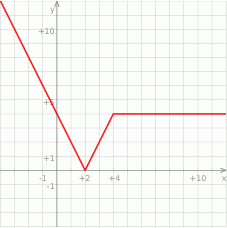
Z obrazka widzimy, że wykres ten ma dokładnie jeden punkt wspólny z prostą 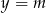y = m dla m ∈ {0} ∪ (4,+ ∞ ) .  
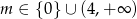Odpowiedź: m ∈ {0} ∪ (4,+ ∞ )

Wersja PDF