Zadanie nr 6620210
Wyznacz wszystkie wartości parametru  , dla których równanie
, dla których równanie 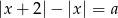 nie ma rozwiązania.
nie ma rozwiązania.
Rozwiązanie
Sposób I
Mamy do rozpatrzenia 3 przypadki.
Jeżeli 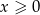 to mamy równanie
to mamy równanie
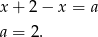
Jeżeli 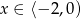 to mamy równanie
to mamy równanie
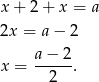
Sprawdźmy jeszcze kiedy to rozwiązanie spełnia warunek 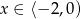 .
.
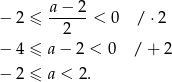
Jeżeli 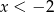 to mamy równanie
to mamy równanie
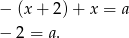
Z powyższych rachunków widać, że równanie ma nieskończenie wiele rozwiązań, gdy 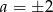 , równanie ma rozwiązanie, gdy
, równanie ma rozwiązanie, gdy 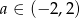 oraz jest sprzeczne w pozostałych przypadkach.
oraz jest sprzeczne w pozostałych przypadkach.
Sposób II
Tym razem narysujemy wykres lewej strony. Aby to zrobić, zapiszmy lewą stronę bez wartości bezwzględnej.
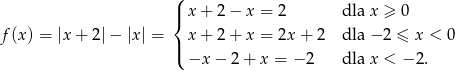
Rysujemy teraz wykres i bez trudu odczytujemy, że równanie 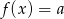 jest sprzeczne jeżeli
jest sprzeczne jeżeli 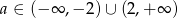 .
.
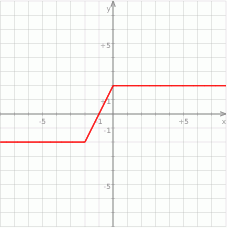
Odpowiedź: