/Szkoła średnia/Równania/Z wartością bezwględną/Liniowe/Z parametrem

Zadanie nr 6662350

Podaj liczbę rozwiązań równania 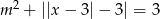2 m + ||x − 3| − 3| = 3 w zależności od wartości parametru m .

Wersja PDF

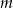Rozwiązanie

Zapiszmy równanie w postaci

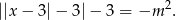
2 ||x − 3| − 3|− 3 = −m .

Rysujemy wykres lewej strony. Zaczynamy od prostej 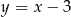y = x− 3 i odbijamy je część poniżej osi 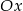Ox do góry. Otrzymany wykres przesuwamy o 3 jednostki w dół i znowu odbijamy część poniżej osi 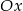Ox do góry. Mamy teraz wykres funkcji 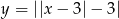y = ||x− 3|− 3| . Na koniec przesuwamy ten wykres o 3 jednostki w dół.

PIC

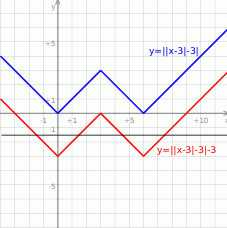
Z wykresu widać, że liczba rozwiązań danego równania jest równa

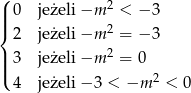
( 2 || 0 jeżeli −m < − 3 |{ 2 jeżeli −m 2 = − 3 2 ||| 3 jeżeli −m = 0 ( 4 jeżeli − 3 < −m 2 < 0

Daje nam to liczbę rozwiązań

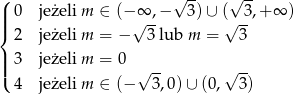
-- -- (| 0 jeżeli m ∈ (− ∞ ,− √ 3)∪ (√ 3,+ ∞ ) ||{ √ -- √ -- 2 jeżeli m = − 3 lub m = 3 || 3 jeżeli m = 0 |( √ -- √ -- 4 jeżeli m ∈ (− 3,0)∪ (0 , 3)

 
Odpowiedź: ( √ -- √ -- | 0 je żeli m ∈ (− ∞ ,− 3) ∪ ( 3,+ ∞ ) ||{ √ -- √ -- 2 je żeli m = − 3 lub m = 3 || 3 je żeli m = 0 |( 4 je żeli m ∈ (− √ 3-,0 )∪ (0,√ 3)

Wersja PDF