Zadanie nr 9238066
Wyznacz te wartości parametru 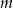 , dla których równanie
, dla których równanie
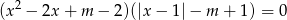
ma dokładnie trzy pierwiastki rzeczywiste? Oblicz te pierwiastki.
Rozwiązanie
Sposób I
Tak naprawdę mamy dwa równania. Sprawdźmy, dla każdego z nich osobno, ile mają pierwiastków.
Najpierw zajmijmy się równaniem
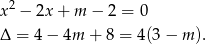
Teraz pora na drugie równanie
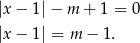
Równanie to ma jedno rozwiązanie dla 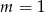 , dwa dla
, dwa dla 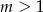 i nie ma rozwiązań dla
i nie ma rozwiązań dla 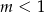 .
.
No dobrze, kiedy wyjściowe równanie będzie miało 3 pierwiastki? – możliwe są dwie sytuacje: albo jedno z równań ma jeden pierwiastek, a drugie dwa; albo oba mają po dwa, ale jeden z pierwiastków jest wspólny. Na mocy powyższej analizy, pierwsza sytuacja może mieć miejsce tylko dla 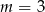 lub
lub 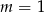 .
.
Jeżeli 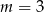 to mamy
to mamy
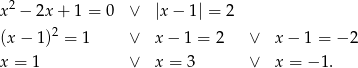
Jeżeli 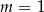 to drugie równanie ma pierwiastek
to drugie równanie ma pierwiastek 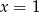 , a równanie kwadratowe
, a równanie kwadratowe
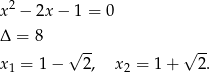
Pozostała do rozpatrzenia sytuacja, gdy oba równania mają po dwa pierwiastki. Pierwiastki drugiego równania łatwo wyznaczyć: są to 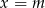 i
i 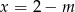 . Sprawdźmy, czy jedna ztych liczb może być pierwiastkiem pierwszego równania.
. Sprawdźmy, czy jedna ztych liczb może być pierwiastkiem pierwszego równania.
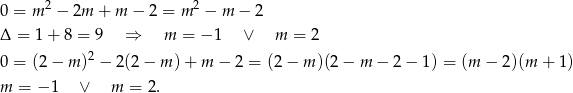
Sprawdzamy te wartości 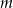 ręcznie. Dla
ręcznie. Dla 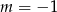 drugie równanie w ogóle nie ma rozwiązań. Jeżeli
drugie równanie w ogóle nie ma rozwiązań. Jeżeli 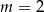 to z drugiego równania mamy
to z drugiego równania mamy 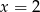 lub
lub 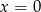 , a pierwsze równania ma postać:
, a pierwsze równania ma postać:
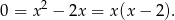
Zatem obydwa pierwiastki są wspólne.
Sposób II
Zadanie można też rozwiązać graficznie. W tym celu zapiszmy podane równanie w postaci
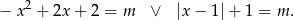
Musimy teraz narysować oba wykresy w układzie współrzędnych i zobaczyć kiedy prosta 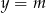 przecina je dokładnie w 3 punktach.
przecina je dokładnie w 3 punktach.
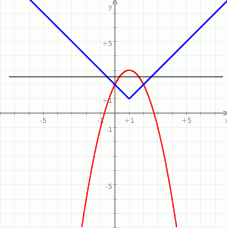
Z wykresu wyraźnie widać, że sytuacja taka ma miejsce dla 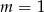 i
i 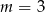 . Pierwiastki znajdujemy jak w poprzednim sposobie.
. Pierwiastki znajdujemy jak w poprzednim sposobie.
Sposób III
Powyższe rozwiązania (szczególnie drugie) pokazują symetryczność całego obrazka względem prostej 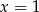 . Spróbujmy tę symetrię wykorzystać. Podstawiając
. Spróbujmy tę symetrię wykorzystać. Podstawiając 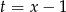 mamy równanie
mamy równanie
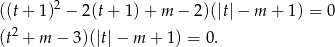
Oba równania mają pierwiastki tylko dla 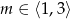 i pierwiastki te są równe
i pierwiastki te są równe
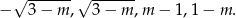
Pytanie brzmi: kiedy są to dokładnie trzy różne liczby? Ponieważ są to dwie pary liczb przeciwnych, tak będzie gdy jedna z nich jest zero (to nam daje 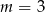 i
i 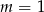 ). Sytuacja
). Sytuacja 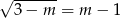 da tylko dwa pierwiastki, bo wtedy
da tylko dwa pierwiastki, bo wtedy 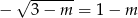 . Dla
. Dla 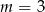 i
i 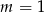 mamy odpowiednio pierwiastki
mamy odpowiednio pierwiastki
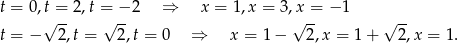
Odpowiedź: 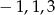 dla
dla 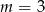 i
i 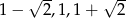 dla
dla