/Szkoła średnia/Geometria/Planimetria/Czworokąt/Prostokąt

Zadanie nr 1504347

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest prostokąt o polu 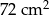2 72 cm . Gdyby zwiększyć długość jednego z boków o 2 cm, a drugi bok zmniejszyć o 3 cm, to pole nie ulegnie zmianie. Oblicz długości boków danego prostokąta.

Rozwiązanie

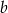Oznaczmy przez a i b długości boków danego prostokąta. Wiemy, że

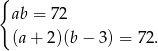
{ ab = 72 (a+ 2)(b− 3) = 72.

Podstawiamy 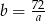72 b = a z pierwszego równania do drugiego.

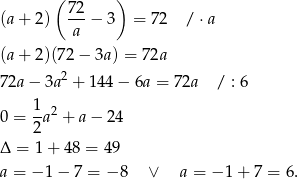
( 72 ) (a+ 2 ) ---− 3 = 72 / ⋅a a (a+ 2 )(72− 3a) = 72a 2 72a− 3a + 144 − 6a = 7 2a / : 6 1 2 0 = -a + a − 24 2 Δ = 1 + 48 = 49 a = − 1− 7 = − 8 ∨ a = − 1 + 7 = 6.

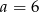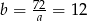Ujemne rozwiązanie odrzucamy i mamy a = 6 . Stąd b = 72 = 12 a .  
Odpowiedź: 6 cm i 12 cm.

Wersja PDF