/Szkoła średnia/Geometria/Planimetria/Czworokąt/Prostokąt

Zadanie nr 1714538

Dodaj do ulubionych
Dodaj do rozwiązanych

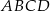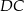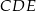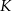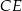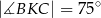Dany jest prostokąt ABCD , którego jeden bok jest dwa razy dłuższy od drugiego. Na boku DC zbudowano trójkąt równoboczny CDE (zobacz rysunek). Punkt K jest takim punktem odcinka CE , że |∡BKC | = 7 5∘ . Udowodnij, że punkt 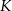K jest środkiem odcinka CE .

PIC

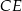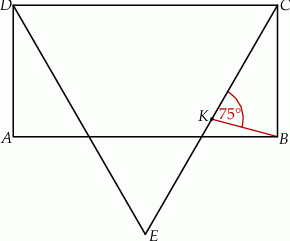
Rozwiązanie

Zauważmy najpierw, że

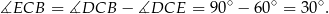
∘ ∘ ∘ ∡ECB = ∡DCB − ∡DCE = 90 − 60 = 30 .

Stąd

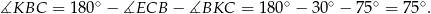
∘ ∘ ∘ ∘ ∘ ∡KBC = 180 − ∡ECB − ∡BKC = 180 − 30 − 75 = 75 .

To oznacza, że trójkąt 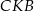CKB jest równoramienny i

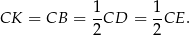
CK = CB = 1CD = 1CE . 2 2

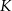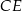Zatem rzeczywiście punkt K jest środkiem odcinka CE .

Wersja PDF