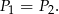Zadanie nr 5678208
Punkt 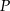 leży wewnątrz prostokąta
leży wewnątrz prostokąta 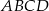 . Wykaż, że suma pól trójkątów
. Wykaż, że suma pól trójkątów 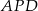 i
i 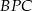 jest równa sumie pól trójkątów
jest równa sumie pól trójkątów 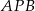 i
i 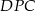 .
.
Rozwiązanie
Zaczynamy od rysunku
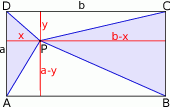
Policzmy najpierw sumę pól trójkątów 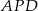 i
i 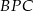
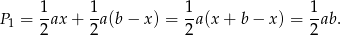
Teraz policzymy sumę pól trójkątów 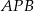 i
i 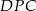
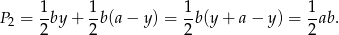
Zatem