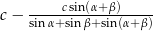Zadanie nr 1530595
W trójkącie 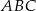 poprowadzono prostą
poprowadzono prostą 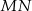 równoległą do prostej
równoległą do prostej 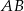 tak, że
tak, że 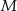 należy do
należy do 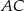 ,
, 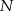 należy do
należy do 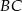 oraz
oraz 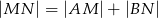 . Oblicz
. Oblicz 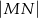 , jeśli
, jeśli 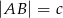 , a miary kątów trójkąta przy boku
, a miary kątów trójkąta przy boku 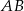 wynoszą
wynoszą  oraz
oraz 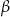 .
.
Rozwiązanie
Zaczynamy od rysunku.
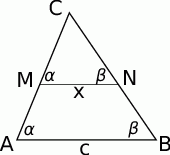
Niech 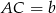 ,
, 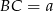 oraz
oraz 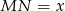 . O liczbach
. O liczbach  i
i 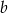 możemy sobie myśleć, że są dane, bo łatwo je wyliczyć z twierdzenia sinusów
możemy sobie myśleć, że są dane, bo łatwo je wyliczyć z twierdzenia sinusów
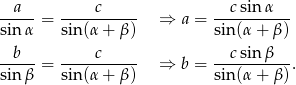
Trójkąty 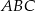 i
i 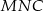 są podobne – oznaczmy ich skalę podobieństwa przez
są podobne – oznaczmy ich skalę podobieństwa przez 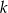 . Mamy
. Mamy
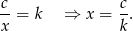
Pozostało wyliczyć skalę podobieństwa 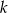 . Aby to zrobić, zauważmy, że obwód trójkąta
. Aby to zrobić, zauważmy, że obwód trójkąta 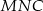 jest równy
jest równy 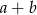 . Rzeczywiście, wynika to natychmiast z warunku
. Rzeczywiście, wynika to natychmiast z warunku 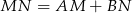 . Możemy zatem wyliczyć
. Możemy zatem wyliczyć 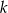 porównując obwody trójkątów
porównując obwody trójkątów 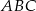 i
i 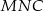 .
.
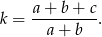
Mamy stąd
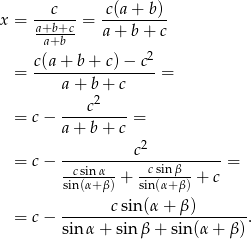
Odpowiedź: