Zadanie nr 1561420
Dany jest okrąg o środku w punkcie 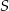 i promieniu
i promieniu  . Na przedłużeniu cięciwy
. Na przedłużeniu cięciwy 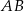 poza punkt
poza punkt 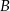 odłożono odcinek
odłożono odcinek 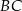 równy promieniowi danego okręgu. Przez punkty
równy promieniowi danego okręgu. Przez punkty 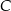 i
i 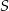 poprowadzono prostą. Prosta
poprowadzono prostą. Prosta 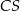 przecina dany okrąg w punktach
przecina dany okrąg w punktach 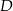 i
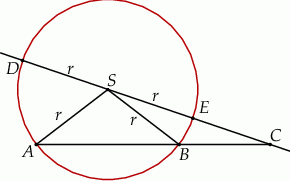
i 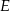 (zobacz rysunek). Wykaż, że jeżeli miara kąta
(zobacz rysunek). Wykaż, że jeżeli miara kąta 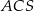 jest równa
jest równa  , to miara kąta
, to miara kąta 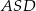 jest równa
jest równa 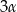 .
.
Rozwiązanie
Z założenia trójkąt 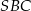 jest równoramienny, więc
jest równoramienny, więc
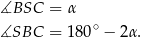
Trójkąt 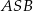 również jest równoramienny, więc
również jest równoramienny, więc
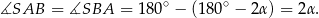
Stąd