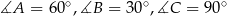Zadanie nr 2005189
Środkowa 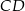 trójkąta
trójkąta 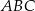 jest równa bokowi
jest równa bokowi 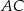 . Wyznacz kąty trójkąta
. Wyznacz kąty trójkąta 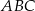 wiedząc, że
wiedząc, że 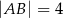 i
i 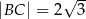 .
.
Rozwiązanie
Zaczynamy od rysunku.
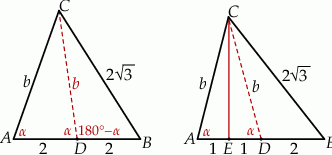
Sposób I
Jeżeli chwilę się zastanowimy nad zadaniem, to łatwo widać, że trójkąt 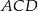 jest równoramienny, czyli
jest równoramienny, czyli 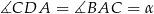 . Trochę trudniej jest wykorzystać informację o tym, że prosta
. Trochę trudniej jest wykorzystać informację o tym, że prosta 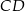 jest środkową. Jeden ze sposobów, to napisanie twierdzeń cosinusów w trójkątach
jest środkową. Jeden ze sposobów, to napisanie twierdzeń cosinusów w trójkątach 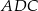 i
i 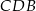 .
.
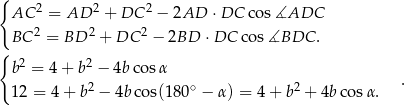
Dodajemy te równania stronami (żeby skrócić 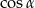 ) i mamy
) i mamy
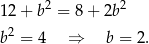
Tak więc trójkąt 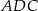 jest równoboczny i wszystkie jego kąty są równe
jest równoboczny i wszystkie jego kąty są równe 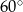 . Trójkąt
. Trójkąt 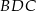 jest równoramienny i
jest równoramienny i 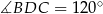 , czyli
, czyli 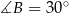 . Zatem
. Zatem
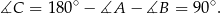
Sposób II
Prostsze rozwiązanie otrzymamy jeżeli dorysujemy wysokość 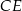 . Ponieważ trójkąt
. Ponieważ trójkąt 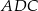 jest równoramienny, wysokość ta dzieli odcinek
jest równoramienny, wysokość ta dzieli odcinek 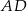 na połowę. W takim razie
na połowę. W takim razie 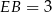 i mamy
i mamy
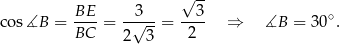
Liczymy dalej.
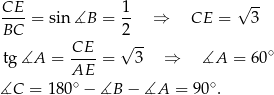
Odpowiedź: