Zadanie nr 2046368
Dany jest okrąg o środku w punkcie 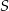 i promieniu
i promieniu  . Na przedłużeniu cięciwy
. Na przedłużeniu cięciwy 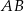 poza punkt
poza punkt 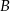 odłożono odcinek
odłożono odcinek 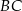 . Przez punkty
. Przez punkty 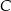 i
i 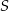 poprowadzono prostą. Prosta
poprowadzono prostą. Prosta 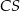 przecina dany okrąg w punktach
przecina dany okrąg w punktach 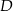 i
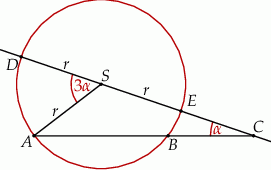
i 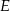 (zobacz rysunek). Wykaż, że jeżeli miara kąta
(zobacz rysunek). Wykaż, że jeżeli miara kąta 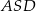 jest trzy razy większa od miary kąta
jest trzy razy większa od miary kąta 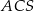 , to
, to 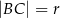 .
.
Rozwiązanie
Dorysujmy promień 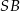 i oznaczmy
i oznaczmy 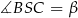 .
.
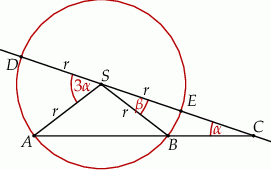
Zauważmy, że wystarczy pokazać, że 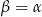 , bo wtedy trójkąt
, bo wtedy trójkąt 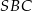 jest równoramienny i
jest równoramienny i 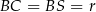 . Liczymy kolejno
. Liczymy kolejno
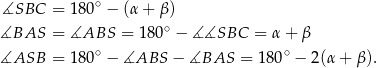
Mamy stąd
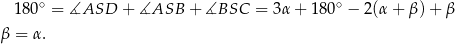
Jak zauważyliśmy wcześniej to oznacza, że 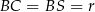 .
.

