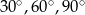/Konkursy/Zadania/Geometria

Zadanie nr 3187517

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz miary kątów trójkąta, w którym wysokość i środkowa poprowadzona z jednego wierzchołka dzielą kąt przy tym wierzchołku na 3 równe części.

Rozwiązanie

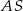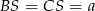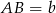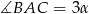Przyjmijmy oznaczenia jak na rysunku, tzn. AS niech będzie środkową, BS = CS = a , AB = b oraz ∡BAC = 3α .

PIC

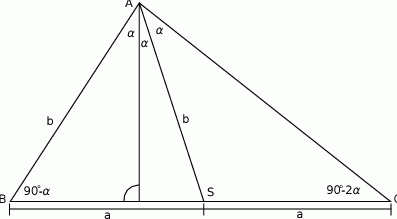
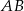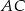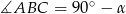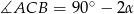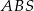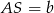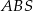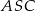Ponieważ wiemy jakie kąty wysokość tworzy z bokami AB i AC , to bez trudu wyliczmy kąty ∡ABC = 90∘ − α oraz ∡ACB = 90∘ − 2α . Ponadto, ponieważ wysokość trójkąta ABS tworzy z bokami równe kąty, trójkąt ten jest równoramienny. Otrzymujemy stąd AS = b . Stosujemy teraz twierdzenie sinusów do trójkątów ABS i ASC otrzymujemy

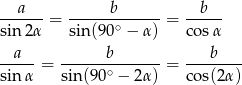
a b b ------= ------∘------= ----- sin 2α sin(90 − α) cosα -a--- ------b------- ---b---- sin α = sin (90∘ − 2α) = cos(2α)

Przekształćmy trochę pierwszą równość (korzystamy ze wzoru 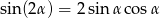sin (2α) = 2 sin α cosα ):

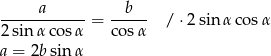
a b ------------= ----- / ⋅2 sin α cosα 2sin αcos α cosα a = 2bsin α

Wstawiając to do drugiej równości otrzymujemy 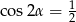cos 2α = 12 , czyli α = 30∘ .  
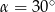Odpowiedź: Kąty trójkąta to ∘ ∘ ∘ 30 ,60 ,90

Wersja PDF