/Konkursy/Zadania/Geometria

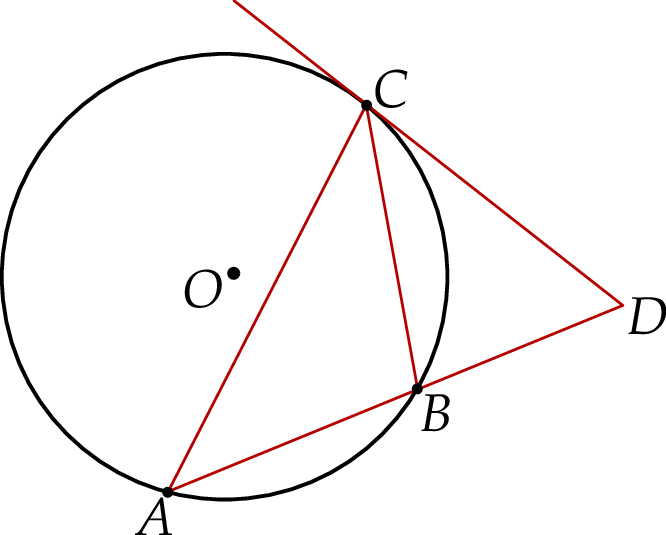
Zadanie nr 3432574

Dodaj do ulubionych
Dodaj do rozwiązanych

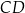Prosta CD jest styczna do okręgu w punkcie 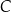C . Uzasadnij, że jeśli 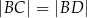|BC | = |BD | , to |AC | = |CD | .

ZINFO-FIGURE

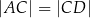Rozwiązanie

Skorzystamy z prostego do uzasadnienia faktu, że cięciwa i styczna to okręgu w końcu tej cięciwy tworzą taki sam kąt jak kąt oparty na tej cięciwie. W naszym przypadku

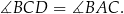
∡BCD = ∡BAC .

Wiemy ponadto, że

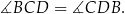
∡BCD = ∡CDB .

Zatem

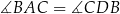
∡BAC = ∡CDB

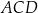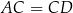i trójkąt ACD jest równoramienny (AC = CD ).

Wersja PDF