Zadanie nr 3689156
Udowodnij, że w trapezie, który ma dwa kąty ostre przy jednej z podstaw, suma kwadratów przekątnych równa jest sumie podwojonego iloczynu dwóch boków równoległych i kwadratów pozostałych boków.
Rozwiązanie
Zaczynamy od rysunku.
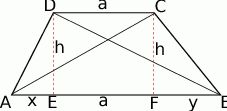
Z trójkątów prostokątnych 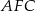 i
i 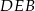 mamy
mamy

Dodając te równości stronami i korzystając z równości 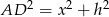 i
i 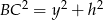 mamy
mamy