Zadanie nr 3814472
Pole trapezu jest równe 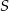 , a stosunek długości jego podstaw wynosi
, a stosunek długości jego podstaw wynosi 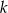 . Przekątne dzielą trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
. Przekątne dzielą trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
Rozwiązanie
Zacznijmy od rysunku i załóżmy, że 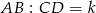 .
.
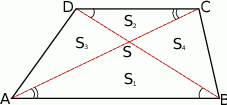
Jedną z najważniejszych własności trapezu, która jest notorycznie wykorzystywana w zadaniach, jest podobieństwo trójkątów 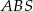 i
i 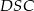 . W dodatku, skala podobieństwa to dokładnie stosunek długości podstaw. Informacja ta oznacza w szczególności, że stosunki pól
. W dodatku, skala podobieństwa to dokładnie stosunek długości podstaw. Informacja ta oznacza w szczególności, że stosunki pól
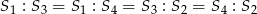
są równe 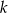 . Aby to zobaczyć, popatrzmy na trójkąty
. Aby to zobaczyć, popatrzmy na trójkąty 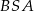 i
i 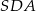 . Mają one wspólną wysokość opuszczoną z wierzchołka
. Mają one wspólną wysokość opuszczoną z wierzchołka 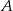 , a stosunek długości podstaw to
, a stosunek długości podstaw to 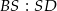 , czyli dokładnie skala podobieństwa trójkątów
, czyli dokładnie skala podobieństwa trójkątów 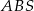 i
i 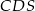 . Podobnie uzasadniamy pozostałe równości. Morał z tego jest taki, że wszystkie pola możemy wyliczyć w zależności od jednego z nich, np. od
. Podobnie uzasadniamy pozostałe równości. Morał z tego jest taki, że wszystkie pola możemy wyliczyć w zależności od jednego z nich, np. od 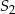 . Mamy
. Mamy
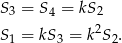
Stąd
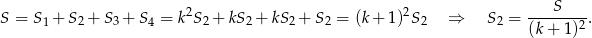
Odpowiedź: