Zadanie nr 4241584
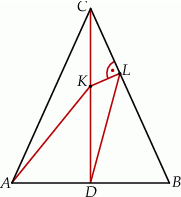
Odcinek 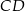 jest wysokością przedstawionego na rysunku trójkąta równoramiennego
jest wysokością przedstawionego na rysunku trójkąta równoramiennego 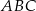 , w którym
, w którym 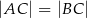 . Punkt
. Punkt 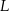 jest rzutem punktu
jest rzutem punktu 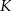 wysokości
wysokości 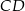 na bok
na bok 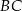 . Udowodnij, że
. Udowodnij, że 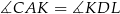 .
.
Rozwiązanie
Dorysujmy odcinek 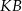 .
.
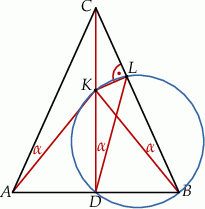
Wysokość 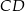 jest osią symetrii trójkąta
jest osią symetrii trójkąta 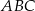 , więc
, więc
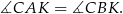
Z drugiej strony, dwa przeciwległe kąty czworokąta 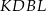 są proste, więc wierzchołki tego czworokąta leżą na jednym okręgu (o średnicy
są proste, więc wierzchołki tego czworokąta leżą na jednym okręgu (o średnicy 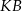 ). Zatem
). Zatem
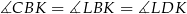
jako kąty wpisane oparte na tym samym łuku.

