Zadanie nr 4383441
W trapezie 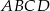 o podstawach
o podstawach 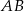 i
i 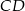 punkt
punkt 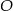 jest punktem wspólnym przekątnych. Oblicz pole trapezu wiedząc, że pole trójkąta
jest punktem wspólnym przekątnych. Oblicz pole trapezu wiedząc, że pole trójkąta 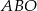 jest równe 5, a pole trójkąta
jest równe 5, a pole trójkąta 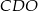 jest równe 4.
jest równe 4.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
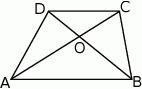
Kluczowa własność trapezu (którą warto zapamiętać) to, że trójkąty 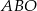 i
i 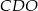 są podobne (mają takie same kąty). W dodatku znamy ich skalę podobieństwa
są podobne (mają takie same kąty). W dodatku znamy ich skalę podobieństwa 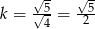 .
.
Jak obliczyć pole trójkąta 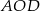 ? Zauważmy, że ma on taką samą wysokość opuszczoną z wierzchołka
? Zauważmy, że ma on taką samą wysokość opuszczoną z wierzchołka 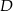 jak trójkąt
jak trójkąt 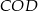 i na mocy wcześniejszej uwagi wiemy jaki jest stosunek ich podstaw. Zatem
i na mocy wcześniejszej uwagi wiemy jaki jest stosunek ich podstaw. Zatem
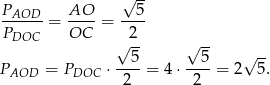
Podobnie obliczamy
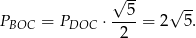
Pole trapezu jest więc równe
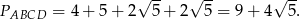
Odpowiedź: