Zadanie nr 4492618
Z przeciwległych wierzchołków prostokąta poprowadzono odcinki prostopadłe do przekątnej. Odcinki te dzielą przekątną na trzy części. Każda z nich jest odcinkiem o długości 4 cm. Oblicz pole tego prostokąta.
Rozwiązanie
Zaczynamy od schematycznego rysunku.
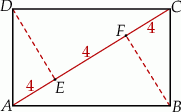
Jeżeli popatrzymy na trójkąt prostokątny 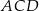 , to wiemy na jakie odcinki dzieli przeciwprostokątną wysokość poprowadzona z wierzchołka
, to wiemy na jakie odcinki dzieli przeciwprostokątną wysokość poprowadzona z wierzchołka 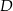 . Ta informacja wystarcza do wyliczenia przyprostokątnych lub, jeżeli ktoś woli, wysokości
. Ta informacja wystarcza do wyliczenia przyprostokątnych lub, jeżeli ktoś woli, wysokości 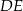 , tego trójkąta. My wyliczymy wysokość
, tego trójkąta. My wyliczymy wysokość 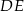 . Patrzymy na trójkąty podobne
. Patrzymy na trójkąty podobne 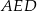 i
i 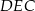 (oba są podobne do trójkąta
(oba są podobne do trójkąta 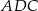 ).
).
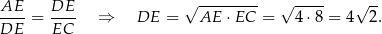
Zatem
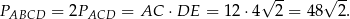
Odpowiedź: