Zadanie nr 5171249
Z punktu 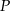 należącego do boku
należącego do boku 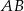 trójkąta równobocznego
trójkąta równobocznego 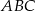 poprowadzono półprostą dzielącą trójkąt na dwie figury o równych polach. Oblicz tangens kąta jaki tworzy ta półprosta z odcinkiem
poprowadzono półprostą dzielącą trójkąt na dwie figury o równych polach. Oblicz tangens kąta jaki tworzy ta półprosta z odcinkiem 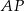 , jeśli
, jeśli 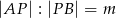 i
i 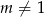 .
.
Rozwiązanie
Zaczynamy oczywiście od rysunku. Oznaczmy długość boku trójkąta przez 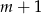 . Dzięki temu
. Dzięki temu 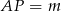 i
i 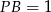 .
.
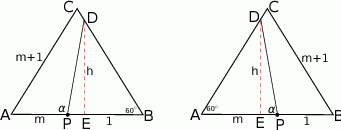
Widać, że możliwe są dwie sytuacje – poprowadzona półprosta może przeciąć bok 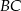 (dla
(dla 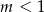 ) lub bok
) lub bok 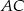 (dla
(dla 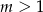 ). Informacja o tym, że półprosta dzieli trójkąt na dwie figury o równych polach oznacza, że pole trójkąta
). Informacja o tym, że półprosta dzieli trójkąt na dwie figury o równych polach oznacza, że pole trójkąta 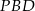 (lub
(lub 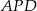 ) jest równe połowie pola całego trójkąta. Zatem
) jest równe połowie pola całego trójkąta. Zatem
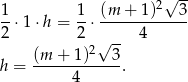
W drugiej sytuacji mamy podobny rachunek.
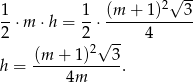
Długość odcinka 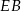 (
(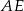 ) wyliczamy z trójkąta prostokątnego
) wyliczamy z trójkąta prostokątnego 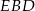 (
(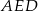 ).
).
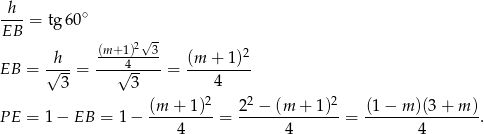
Podobny rachunek mamy w drugim przypadku
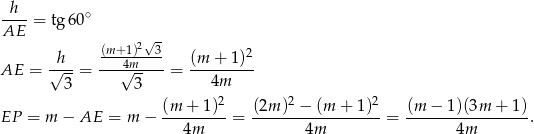
Możemy teraz policzyć szukany tangens.
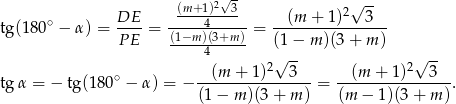
Podobnie w drugim przypadku.
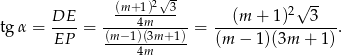
Na koniec uwaga, że tak naprawdę mogliśmy zajmować się tylko przypadkiem 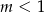 – wzór w przypadku
– wzór w przypadku 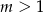 można wtedy otrzymać zamieniając
można wtedy otrzymać zamieniając 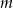 na
na 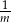 (odbijając trójkąt względem pionowej prostej).
(odbijając trójkąt względem pionowej prostej).
Odpowiedź: 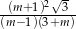 dla
dla 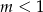 i
i 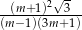 dla
dla