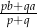/Konkursy/Zadania/Geometria

Zadanie nr 6154744

Dodaj do ulubionych
Dodaj do rozwiązanych

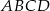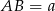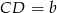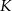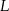Podstawy trapezu ABCD mają długości AB = a i CD = b . Na ramionach trapezu wybrano punkty K i L w ten sposób, że odcinek 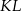KL jest równoległy do podstaw oraz 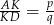AKKD- = pq . Oblicz długość odcinka KL .

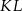Rozwiązanie

Niech 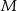M będzie punktem przecięcia odcinka 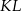KL z przekątną AC .

PIC

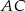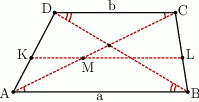
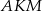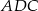Trójkąty AKM i ADC są podobne (mają równe kąty) i skala podobieństwa jest równa

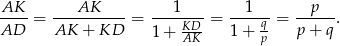
AK--= ---AK----- = ---1---= --1--- = --p---. AD AK + KD 1+ KD- 1 + -q p + q AK p

Zatem

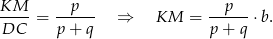
KM p p ---- = ------ ⇒ KM = ------⋅b. DC p + q p + q

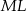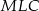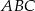Podobnie obliczamy długość odcinka ML . Patrzymy teraz na trójkąty podobne MLC i ABC . Skala ich podobieństwa jest równa

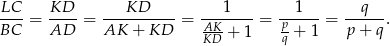
LC KD KD 1 1 q ----= ---- = ----------= --------= p-----= -----. BC AD AK + KD AKKD-+ 1 q + 1 p+ q

Zatem

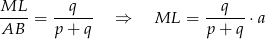
ML-- --q--- --q--- AB = p + q ⇒ ML = p + q ⋅a

oraz

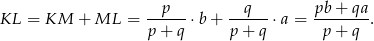
KL = KM + ML = --p---⋅ b+ --q---⋅a = pb-+--qa. p + q p+ q p + q

 
Odpowiedź: pb+qa p+q

Wersja PDF