/Konkursy/Zadania/Geometria

Zadanie nr 6768127

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz długości boków trójkąta wiedząc, że są one kolejnymi liczbami naturalnymi zaś największy kąt jest dwa razy większy od kąta najmniejszego.

Rozwiązanie

Oznaczmy długość boku leżącego naprzeciwko α przez x .

PIC

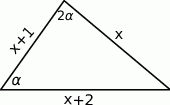
Ponieważ naprzeciwko największego kąta leży najdłuższy bok, to bok naprzeciwko 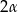2α ma długość 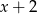x+ 2 , a trzeci z boków długość 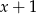x + 1 . Na mocy twierdzenia sinusów mamy

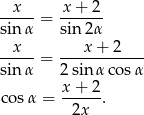
--x-- -x+--2 sinα = sin 2α x x + 2 ----- = ------------ sinα 2 sinα cos α co sα = x+--2. 2x

Z drugiej strony, na mocy twierdzenia cosinusów

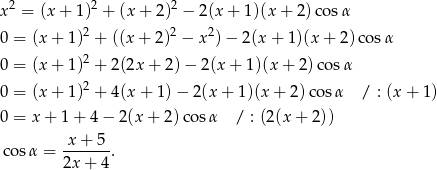
2 2 2 x = (x + 1 ) + (x + 2 ) − 2(x + 1 )(x+ 2)cos α 0 = (x + 1 )2 + ((x + 2)2 − x2) − 2(x + 1)(x + 2)cos α 0 = (x + 1 )2 + 2(2x + 2)− 2(x+ 1)(x + 2)co sα 2 0 = (x + 1 ) + 4(x + 1 )− 2 (x + 1)(x+ 2)cos α / : (x+ 1) 0 = x + 1 + 4 − 2(x + 2 )cos α / : (2 (x+ 2)) x + 5 co sα = ------. 2x + 4

Porównując wyliczone wartości 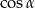cos α otrzymujemy

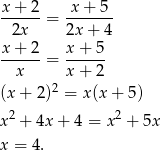
x + 2 x+ 5 ------= ------- 2x 2x + 4 x-+-2-= x-+-5- x x + 2 (x + 2)2 = x (x+ 5) x2 + 4x + 4 = x2 + 5x x = 4 .

 
Odpowiedź: 4,5,6

Wersja PDF