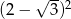Zadanie nr 6918455
Ramiona kąta o mierze 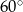 przecięto prostą
przecięto prostą  prostopadłą do jednego z ramion kąta i wpisano dwa koła styczne do obu ramion tego kąta i prostej
prostopadłą do jednego z ramion kąta i wpisano dwa koła styczne do obu ramion tego kąta i prostej 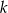 . Oblicz stosunek pól tych kół.
. Oblicz stosunek pól tych kół.
Rozwiązanie
Zaczynijmy od rysunku i oznaczmy 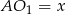 .
.
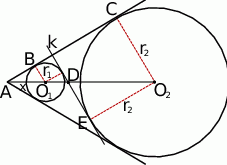
Pomysł na rozwiązanie zadania jest następujący. Musimy jakoś wykorzystać fakt, że okręgi są jednocześnie styczne do ramion kąta i do prostej 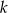 . Własności te pozwolą nam na dwa sposoby wyliczyć długość odcinka
. Własności te pozwolą nam na dwa sposoby wyliczyć długość odcinka  w zależności od
w zależności od 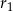 i
i 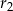 , to da nam szukaną zależność między
, to da nam szukaną zależność między 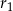 i
i 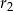 .
.
Po pierwsze, z trójkąta 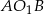 mamy
mamy
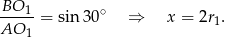
Podobnie uzasadniamy, że 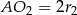 .
.
Drugi sposób wyliczenia  to równość
to równość
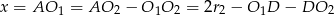
Długości odcinków 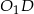 i
i 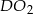 wyliczamy następująco. Z trójkąta
wyliczamy następująco. Z trójkąta 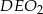 mamy
mamy
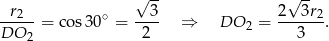
Podobnie
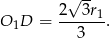
Mamy zatem
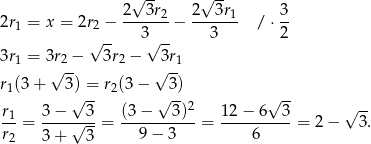
Oczywiście stosunek pól jest równy kwadratowi stosunku promieni, czyli 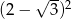 .
.
Odpowiedź: