Zadanie nr 7037217
Narysuj przekrój równoległościanu płaszczyzną 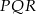 .
.
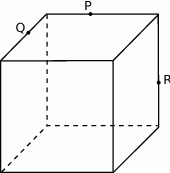
Rozwiązanie
Łatwo jest zacząć – na pewno w przekroju będą odcinki 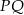 i
i 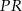 .
.
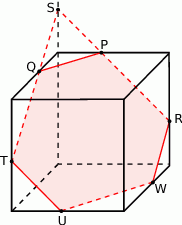
Kolejny krok jest jednak bardzo trudny. Radzę, żebyście spróbowali sobie porysować co ma wyjść - po chwili powinno być jasne, że ma wyjść sześciokąt 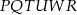 taki, że
taki, że 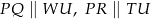 i
i 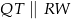 . Pytanie jednak brzmi jak to dokładnie narysować?
. Pytanie jednak brzmi jak to dokładnie narysować?
Pomysł jest następujący. Powiedzmy, że chcemy narysować prostą 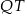 (czyli wyznaczyć punkt
(czyli wyznaczyć punkt 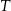 ). Znamy jeden punkt na tej prostej:
). Znamy jeden punkt na tej prostej: 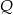 . Jak znaleźć drugi punkt tej prostej? – wystarczy zauważyć, że proste
. Jak znaleźć drugi punkt tej prostej? – wystarczy zauważyć, że proste 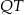 i
i 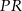 przecinają się w punkcie
przecinają się w punkcie 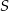 , który leży na przedłużeniu krawędzi sześcianu – tak jest, bo punkt
, który leży na przedłużeniu krawędzi sześcianu – tak jest, bo punkt 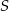 jest po prostu jedynym punktem wspólnym szukanej płaszczyzny i prostej zawierającej tę krawędź sześcianu.
jest po prostu jedynym punktem wspólnym szukanej płaszczyzny i prostej zawierającej tę krawędź sześcianu.
Z powyższej obserwacji wynika następująca konstrukcja: znajdujemy punkt wspólny 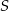 prostej
prostej 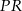 i przedłużenia krawędzi sześcianu (jak na rysunku). Prowadzimy prostą
i przedłużenia krawędzi sześcianu (jak na rysunku). Prowadzimy prostą 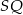 i znajdujemy jej punkt wspólny
i znajdujemy jej punkt wspólny 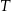 z brzegiem sześcianu. Prowadzimy odcinek
z brzegiem sześcianu. Prowadzimy odcinek 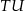 równoległy do prostej
równoległy do prostej 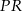 . Prowadzimy odcinek
. Prowadzimy odcinek 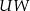 równoległy do prostej
równoległy do prostej 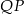 . Otrzymany sześciokąt
. Otrzymany sześciokąt 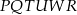 jest szukanym przekrojem sześcianu.
jest szukanym przekrojem sześcianu.

