Zadanie nr 7187004
Na bokach 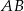 ,
, 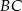 i
i 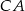 trójkąta
trójkąta 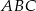 wybrano odpowiednio punkty
wybrano odpowiednio punkty 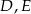 i
i 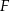 . Wykaż, że okręgi opisane na trójkątach
. Wykaż, że okręgi opisane na trójkątach 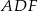 ,
, 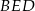 i
i 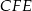 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Rozwiązanie
Szkicujemy opisaną sytuację.
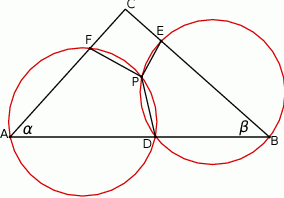
Jeżeli 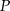 jest punktem wspólnym okręgów opisanych na trójkątach
jest punktem wspólnym okręgów opisanych na trójkątach 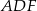 i
i 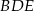 , to wystarczy udowodnić, że na czworokącie
, to wystarczy udowodnić, że na czworokącie 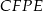 można opisać okrąg. Niech
można opisać okrąg. Niech 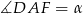 i
i 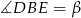 . Czworokąt
. Czworokąt 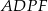 jest wpisany w okrąg, więc
jest wpisany w okrąg, więc
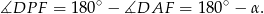
Analogicznie, w czworokącie 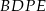 ,
,
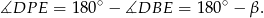
W takim razie
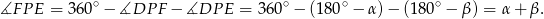
Stąd
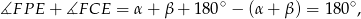
czyli na czworokącie 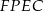 można okrąg. To oznacza, że punkt
można okrąg. To oznacza, że punkt 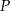 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 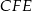 .
.

