/Konkursy/Zadania/Geometria

Zadanie nr 7770287

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że jeżeli 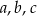a,b,c są długościami boków trójkąta leżącymi naprzeciwko odpowiednio kątów o miarach 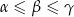α ≤ β ≤ γ to a ≤ b ≤ c .

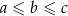Rozwiązanie

Naszkicujmy trójkąt.

PIC

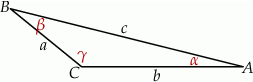
Na mocy twierdzenia sinusów mamy

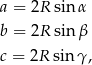
a = 2R sinα b = 2R sinβ c = 2R sinγ ,

gdzie 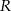R jest promieniem okręgu opisanego na trójkącie.

W przypadku trójkąta ostrokątnego jest to w zasadzie koniec zadania, bo korzystając z tego, że funkcja 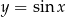y = sin x jest rosnąca w przedziale 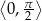⟨ ⟩ 0 , π 2 otrzymujemy stąd a ≤ b ≤ c .

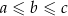Nie mamy jednak założenia, że trójkąt jest ostrokątny, więc musimy się trochę bardziej wysilić.

Załóżmy dalej, że 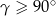γ ≥ 90∘ . Przy tym założeniu mamy

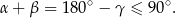
α + β = 1 80∘ − γ ≤ 90 ∘.

To oznacza, że kąty 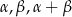α,β,α + β są z I ćwiartki i możemy dla nich skorzystać z monotoniczności sinusa.

sin α ≤ sin β ≤ sin(α + β ) = sin(180∘ − (α + β)) = sin γ / ⋅2R 2R sin α ≤ 2R sin β ≤ 2R sin γ a ≤ b ≤ c.
Wersja PDF