/Konkursy/Zadania/Geometria

Zadanie nr 8866830

Dodaj do ulubionych
Dodaj do rozwiązanych

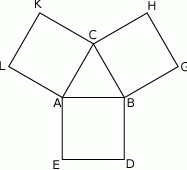
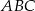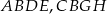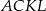Na bokach trójkąta równobocznego ABC (na zewnątrz tego trójkąta) zbudowano kwadraty ABDE ,CBGH i ACKL . Udowodnij, że trójkąt 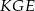KGE jest równoboczny.

PIC

Rozwiązanie

Sposób I

Dorysujmy odcinki 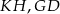KH ,GD i EL .

PIC

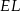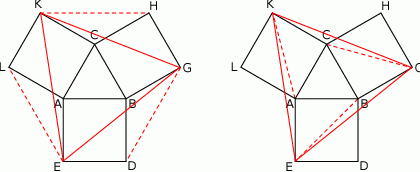
Zauważmy, że każdy z trójkątów: 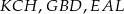KCH ,GBD ,EAL jest równoramienny z ramieniem długości 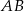AB . Ponadto

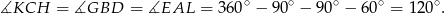
∡KCH = ∡GBD = ∡EAL = 36 0∘ − 90∘ − 90∘ − 60∘ = 12 0∘.

Trójkąty te są więc przystające. To oznacza, że przystające są też trójkąty 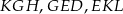KGH ,GED ,EKL . Rzeczywiście

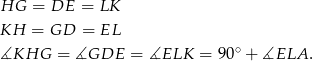
HG = DE = LK KH = GD = EL ∡KHG = ∡GDE = ∡ELK = 90 ∘ + ∡ELA .

To z kolei oznacza, że 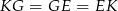KG = GE = EK .

Sposób II

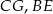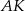Tym razem dorysujmy odcinki CG ,BE i AK . Każdy z tych odcinków ma długość równą przekątnej kwadratu o boku 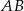AB . Ponadto

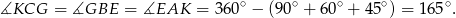
∡KCG = ∡GBE = ∡EAK = 360 ∘ − (9 0∘ + 6 0∘ + 45∘) = 165 ∘.

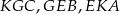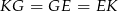To oznacza, że trójkąty KGC ,GEB ,EKA są przystające, czyli KG = GE = EK .

Sposób III

Niech 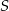S będzie środkiem trójkąta równobocznego ABC .

PIC

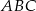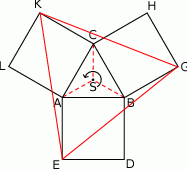
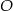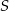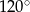Oznaczmy przez O obrót płaszczyzny względem punktu S o kąt 1 20∘ . Oczywiście

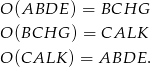
O(ABDE ) = BCHG O(BCHG ) = CALK O(CALK ) = ABDE .

W szczególności, obrót 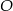O przekształca trójkąt 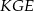KGE na ten sam trójkąt. To oznacza, że trójkąt ten jest równoboczny (tak jest, bo np. kąty trójkąta muszą być równe – obrót 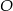O przekształca je kolejno na siebie).

Wersja PDF