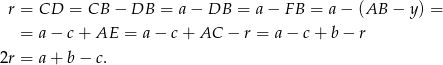Zadanie nr 9178905
Przyprostokątne trójkąta prostokątnego mają długości  i
i 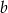 , a jego przeciwprostokątna ma długość
, a jego przeciwprostokątna ma długość  . Wykaż, że promień okręgu wpisanego w ten trójkąt ma długość
. Wykaż, że promień okręgu wpisanego w ten trójkąt ma długość 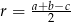 .
.
Rozwiązanie
Sposób I
Szkicujemy trójkąt.
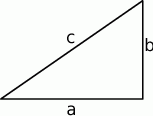
Promień  okręgu wpisanego możemy wyliczyć ze wzoru na pole
okręgu wpisanego możemy wyliczyć ze wzoru na pole
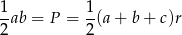
Mamy zatem
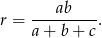
Pozostaje wykazać, że
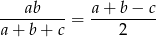
Przekształcamy w sposób równoważny
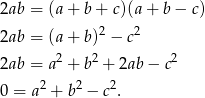
Otrzymana równość jest oczywiście spełniona (jest to twierdzenie Pitagorasa).
Sposób II
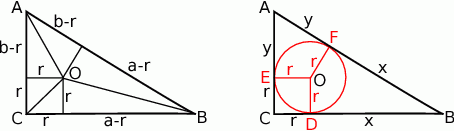
Jeżeli połączymy środek 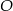 okręgu wpisanego w trójkąt prostokątny
okręgu wpisanego w trójkąt prostokątny 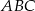 z jego wierzchołkami, to odcinki te dzielą kąty trójkąta na połowy. Jeżeli dorysujemy jeszcze rzuty punktu
z jego wierzchołkami, to odcinki te dzielą kąty trójkąta na połowy. Jeżeli dorysujemy jeszcze rzuty punktu 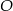 na boki trójkąta, to mamy trzy pary przystających trójkątów prostokątnych. Oznaczając odpowiednio ich boki, widać, że
na boki trójkąta, to mamy trzy pary przystających trójkątów prostokątnych. Oznaczając odpowiednio ich boki, widać, że
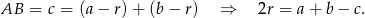
Sposób III
Dorysujmy okrąg wpisany i oznaczmy jego punkty styczności z bokami trójkąta przez 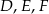 . Mamy zatem
. Mamy zatem