Zadanie nr 9405866
Podstawy trapezu 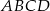 mają długości
mają długości 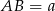 i
i 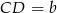 . Na ramionach trapezu wybrano punkty
. Na ramionach trapezu wybrano punkty 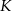 i
i 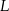 w ten sposób, że odcinek
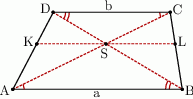
w ten sposób, że odcinek 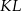 jest równoległy do podstaw i przechodzi przez punkt przecięcia przekątnych. Oblicz długość odcinka
jest równoległy do podstaw i przechodzi przez punkt przecięcia przekątnych. Oblicz długość odcinka 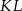 .
.
Rozwiązanie
Zauważmy, że trójkąty 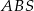 i
i 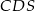 są podobne (bo mają równe kąty).
są podobne (bo mają równe kąty).
Znamy ponadto skalę ich podobieństwa:
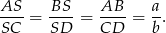
Zauważmy teraz, że trójkąty 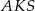 i
i 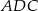 są podobne i możemy wyliczyć ich skalę podobieństwa:
są podobne i możemy wyliczyć ich skalę podobieństwa:
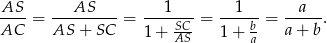
Zatem
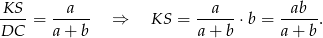
Dokładnie w ten sam sposób obliczamy długość odcinka 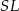 (patrzymy na trójkąty podobne
(patrzymy na trójkąty podobne 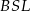 i
i 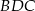 ). Stąd
). Stąd
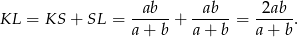
Odpowiedź: