/Konkursy/Zadania/Geometria

Zadanie nr 9500900

Dodaj do ulubionych
Dodaj do rozwiązanych

Na bokach trójkąta równobocznego zbudowano dwa kwadraty w sposób pokazany na rysunku.

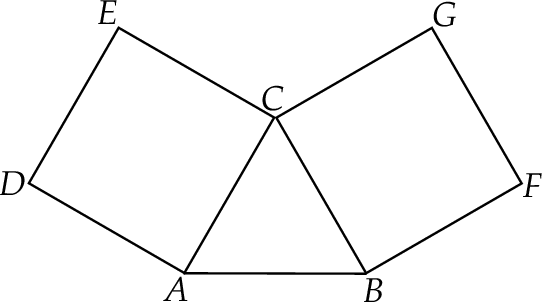
ZINFO-FIGURE

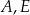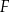Wykaż, że punkty A ,E i F są wierzchołkami trójkąta prostokątnego.

Rozwiązanie

Dorysujmy trójkąt 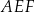AEF .

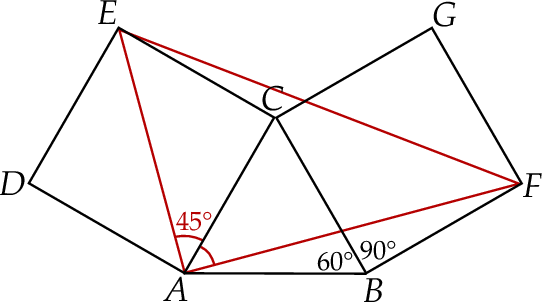
ZINFO-FIGURE

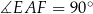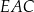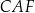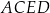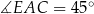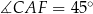Pokażemy, że ∡EAF = 90∘ . Zauważmy, że kąt ten możemy podzielić na dwa kąty EAC i CAF . Pierwszy z nich to kąt między przekątną, a bokiem w kwadracie ACED , więc ∡EAC = 45∘ . Pozostało zatem wykazać, że ∘ ∡CAF = 45 .

Zauważmy, że trójkąt 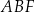ABF jest równoramienny, oraz

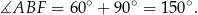
∡ABF = 60∘ + 90∘ = 150∘.

Zatem

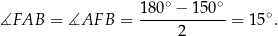
∘ ∘ ∡FAB = ∡AF B = 180--−-15-0- = 15∘ . 2

Zatem

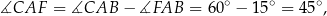
∡CAF = ∡CAB − ∡FAB = 60∘ − 15∘ = 45∘,

co kończy uzasadnienie.

Wersja PDF