Zadanie nr 9630167
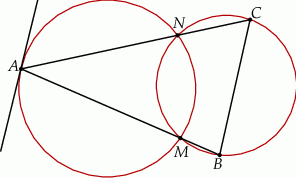
Dwa okręgi przecinają się w punktach 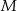 i
i 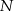 . Przez punkt
. Przez punkt 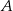 pierwszego okręgu prowadzimy proste
pierwszego okręgu prowadzimy proste 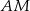 i
i 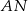 , przecinające drugi okrąg w punktach
, przecinające drugi okrąg w punktach 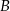 i
i 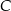 . Udowodnij, że styczna w punkcie
. Udowodnij, że styczna w punkcie 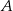 do pierwszego okręgu jest równoległa do prostej
do pierwszego okręgu jest równoległa do prostej 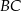 .
.
Rozwiązanie
Dorysujmy odcinek 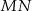 i oznaczmy
i oznaczmy 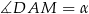 .
.
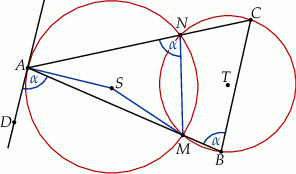
Sposób I
Na mocy twierdzenia o stycznej i siecznej, mamy
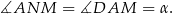
Stąd
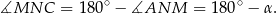
Czworokąt 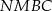 jest wpisany w okrąg, więc
jest wpisany w okrąg, więc
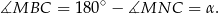
To oznacza, że proste 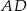 i
i 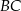 przecinają prostą
przecinają prostą 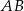 pod takim samym kątem, czyli są równoległe.
pod takim samym kątem, czyli są równoległe.
Sposób II
Tym razem nie będziemy korzystać z twierdzenia o stycznej i siecznej – zamiast tego dorysujmy promienie 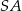 i
i 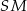 . Promień
. Promień 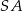 jest prostopadły do stycznej, więc
jest prostopadły do stycznej, więc
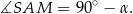
Trójkąt 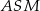 jest równoramienny, więc
jest równoramienny, więc
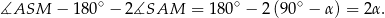
Kąty 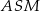 i
i 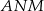 są oparte na tym samym łuku, więc
są oparte na tym samym łuku, więc
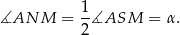
Teraz wystarczy skorzystać z tego, że czworokąt 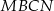 jest wpisany w okrąg.
jest wpisany w okrąg.
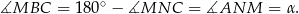
To oznacza, że proste 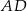 i
i 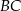 przecinają prostą
przecinają prostą 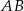 pod takim samym kątem, czyli są równoległe.
pod takim samym kątem, czyli są równoległe.

