Zadanie nr 9636315
Czworokąty 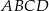 i
i 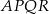 są kwadratami. Udowodnij, że
są kwadratami. Udowodnij, że 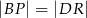 .
.
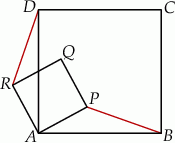
Rozwiązanie
Sposób I
Jak się chwilę zastanowimy, to można zauważyć, że tak naprawdę mamy udowodnić przystawanie trójkątów 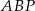 i
i 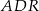 (mają one dwa boki równe i mamy udowodnić, że trzecie boki też są równe). Aby to zrobić, wystarczy pokazać, że
(mają one dwa boki równe i mamy udowodnić, że trzecie boki też są równe). Aby to zrobić, wystarczy pokazać, że 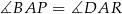 . To jednak jest dość proste. Patrząc na kwadrat
. To jednak jest dość proste. Patrząc na kwadrat 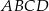 mamy
mamy
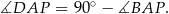
Jeżeli teraz popatrzymy na kwadrat 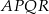 to
to
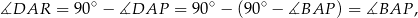
co kończy dowód.
Mogliśmy też równość kątów 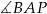 i
i 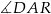 uzasadnić następująco
uzasadnić następująco
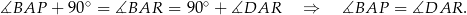
Sposób II
Niech 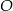 będzie obrotem płaszczyzny o kąt
będzie obrotem płaszczyzny o kąt 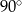 (obracamy o kąt dodatni, czyli w lewo) względem punktu
(obracamy o kąt dodatni, czyli w lewo) względem punktu 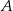 . W takim razie
. W takim razie 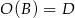 i
i 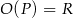 . To oznacza, że
. To oznacza, że 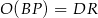 , czyli odcinki te mają równe długości (obrót jest izometrią – zachowuje długość odcinków).
, czyli odcinki te mają równe długości (obrót jest izometrią – zachowuje długość odcinków).

