/Konkursy/Zadania/Geometria/Planimetria

Zadanie nr 1190516

Dodaj do ulubionych
Dodaj do rozwiązanych

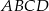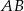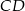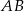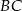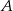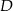Dany jest trapez prostokątny ABCD o podstawach AB i CD , w którym boki AB i BC są prostopadłe. Dwusieczne kątów A i D przecinają się w punkcie 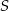S leżącym na boku 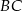BC . Wykaż, że |BS | = |SC | .

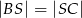Rozwiązanie

Rozpoczynamy od rysunku.

PIC

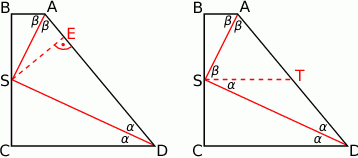
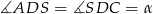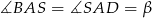Oznaczmy ∡ADS = ∡SDC = α i ∡BAS = ∡SAD = β .

Sposób I

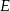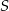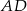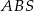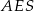Niech E będzie rzutem punktu S na prostą AD . Zauważmy, że trójkąty ABS i AES są oba prostokątne, każdy z nich ma kąt ostry o mierze 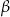β oraz mają wspólną przeciwprostokątną 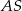AS . Są więc przystające, czyli

BS = ES .

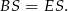
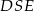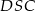Analogicznie uzasadniamy, że trójkąty prostokątne DSE i DSC są przystające. Stąd

SC = ES .

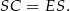
Zatem rzeczywiście 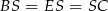BS = ES = SC .

Sposób II

Zauważmy, że

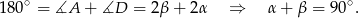
1 80∘ = ∡A + ∡D = 2β + 2 α ⇒ α + β = 90∘.

To oznacza, że trójkąt 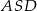ASD jest prostokątny, bo

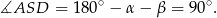
∘ ∘ ∡ASD = 180 − α − β = 90 .

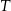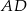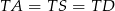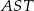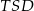Niech T będzie środkiem odcinka AD . Ponieważ w trójkącie prostokątnym środek przeciwprostokątnej jest środkiem okręgu opisanego mamy wtedy TA = TS = TD , czyli trójkąty AST i TSD są równoramienne. To oznacza, że

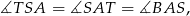
∡T SA = ∡SAT = ∡BAS ,

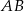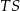czyli proste AB i T S są równoległe (przecinają prostą 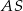AS pod tym samym kątem). Na mocy twierdzenia Talesa

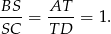
BS AT SC-= T-D-= 1.

Sposób III

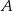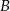Tym razem odbijmy punkty A i B względem prostej BC .

PIC

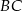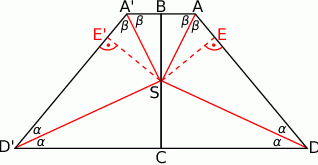
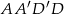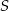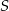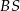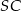Otrzymujemy w ten sposób trapez równoramienny ′ ′ AA D D , w którym dwusieczne wszystkich kątów wewnętrznych przecinają się w jednym punkcie S . To oznacza, że w trapez ten można wpisać okrąg i środkiem tego okręgu jest punkt S . Odcinki BS i SC są promieniami tego okręgu, więc rzeczywiście

BS = SC .
Wersja PDF