Zadanie nr 1195313
W trójkącie równoramiennym 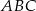 (
(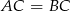 ) poprowadzono wysokości
) poprowadzono wysokości 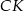 i
i 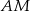 . Wiedząc że
. Wiedząc że 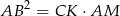 wyznacz cosinus kąta przy podstawie trójkąta.
wyznacz cosinus kąta przy podstawie trójkąta.
Rozwiązanie
Tradycyjnie zaczynamy od rysunku.
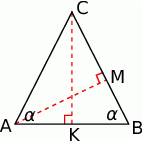
Sposób I
Przekształcimy podaną równość tak, aby były w niej tylko funkcje trygonometryczne kąta  .
.
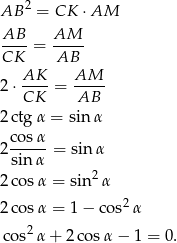
Po podstawieniu 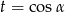 dostajemy zwykłe równanie kwadratowe, które ma dwa rozwiązania
dostajemy zwykłe równanie kwadratowe, które ma dwa rozwiązania 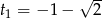 i
i 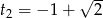 . Ponieważ
. Ponieważ 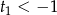 , pierwsze z tych rozwiązań odrzucamy.
, pierwsze z tych rozwiązań odrzucamy.
Sposób II
Musimy jakoś związać ze sobą dwie wysokości 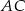 i
i 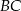 , żeby wykorzystać podany warunek. Możliwości jest kilka, np.
, żeby wykorzystać podany warunek. Możliwości jest kilka, np.
- z podobieństwa trójkątów
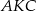 i
i 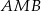 mamy
mamy 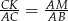 ,
, - porównanie dwóch wzorów na pole trójkąta:
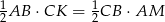 .
.
Tak czy inaczej, dostajemy
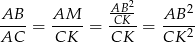
Ponieważ nie widać specjalnie co z tym dalej zrobić, zacznijmy liczyć 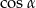 . Liczymy to z trójkąta prostokątnego
. Liczymy to z trójkąta prostokątnego 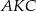 .
.
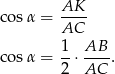
Możemy teraz skorzystać z wcześniej wyliczonej równości
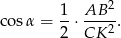
Aby kontynuować te rachunki zauważmy, że
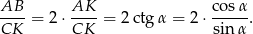
Mamy zatem
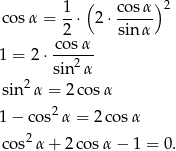
Równanie to rozwiązujemy tak jak w sposobie I.
Odpowiedź: