/Konkursy/Zadania/Geometria/Planimetria

Zadanie nr 1679087

Dodaj do ulubionych
Dodaj do rozwiązanych

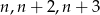Wykaż, że istnieją dokładnie dwie liczby naturalne n takie, że trójkąt o bokach n ,n+ 2,n + 3 jest rozwartokątny.

Rozwiązanie

Ponieważ w trójkącie naprzeciwko większego kąta leży większy bok, to kąt rozwarty α musi być naprzeciwko boku długości n+ 3 .

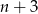Sposób I

Na mocy twierdzenia cosinusów mamy

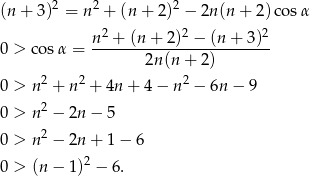
(n + 3)2 = n2 + (n + 2)2 − 2n (n+ 2)co sα n-2 +-(n-+-2)2 −-(n-+-3)2 0 > cos α = 2n(n + 2) 0 > n2 + n 2 + 4n + 4− n 2 − 6n− 9 2 0 > n − 2n − 5 0 > n2 − 2n + 1 − 6 2 0 > (n − 1) − 6.

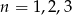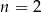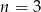Widać, że nierówność ta jest spełniona tylko dla n = 1,2,3 . Ponieważ z odcinków 1,3,4 nie da się zbudować trójkąta (bo 4=3+1), tylko dla n = 2 lub n = 3 istnieje trójkąt spełniający warunki zadania.

Sposób II

Korzystamy z tego, że trójkąt o bokach 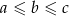a ≤ b ≤ c jest trójkątem rozwartokątnym wtedy i tylko wtedy, gdy 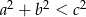a2 + b2 < c2 (tak naprawdę udowodniliśmy tę własność w I sposobie). Rozwiązujemy więc nierówność

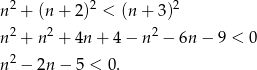
2 2 2 n + (n + 2) < (n + 3) n 2 + n 2 + 4n+ 4− n2 − 6n − 9 < 0 2 n − 2n − 5 < 0.

Dalszą część rozwiązania prowadzimy dokładnie tak samo jak w I sposobie.

Wersja PDF