/Konkursy/Zadania/Geometria/Planimetria

Zadanie nr 1837133

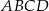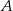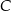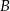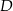Wykaż, że jeżeli w czworokącie ABCD dwusieczne kątów przy wierzchołkach A i C przecinają dwusieczne kątów przy wierzchołkach B i D w czterech różnych punktach, to punkty te leżą na pewnym okręgu.

Wersja PDF

Rozwiązanie

Zaczynamy od rysunku.

PIC

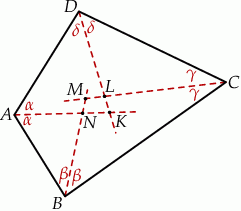
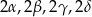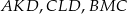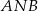Oznaczymy kąty czworokąta przez 2α,2β ,2γ,2δ . Patrząc na trójkąty AKD ,CLD ,BMC i ANB łatwo wyliczamy kąty czworokąta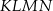 KLMN

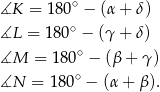
∘ ∡K = 1 80 − (α+ δ) ∡L = 18 0∘ − (γ + δ) ∘ ∡M = 180 − (β + γ) ∡N = 180∘ − (α + β).

Z równości tych łatwo zobaczyć, że

∡K + ∡M = ∡L + ∡N .

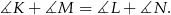
I to koniec, bo równość sum miar przeciwległych kątów to warunek wystarczający na to, aby na czworokącie dało się opisać okrąg.

Wersja PDF