Zadanie nr 3005315
Jedna z podstaw trapezu wpisanego w okrąg jest średnicą okręgu. Oblicz cosinus kąta ostrego trapezu wiedząc, że stosunek obwodu trapezu do sumy długości jego podstaw wynosi 3:2.
Rozwiązanie
Sposób I
Zaczynamy od rysunku.
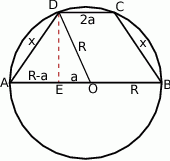
Trapez wpisany w okrąg musi być równoramienny, oznaczmy długość jego ramienia przez  . Mamy zatem
. Mamy zatem
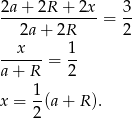
Napiszmy teraz twierdzenie cosinusów w trójkącie 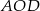 .
.
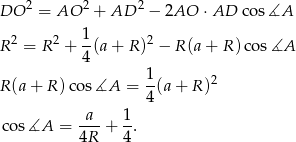
Aby wyliczyć iloraz 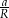 , napiszmy twierdzenie Pitagorasa w trójkątach
, napiszmy twierdzenie Pitagorasa w trójkątach 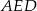 i
i 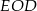 .
.
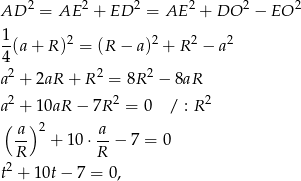
gdzie 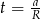 . Dalej,
. Dalej, 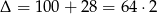 , Dodatni pierwiastek to
, Dodatni pierwiastek to 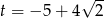 . Stąd
. Stąd
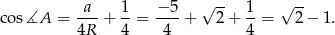
Sposób II
Podobnie jak poprzednio zauważamy, że 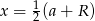 .
.
Zauważmy jeszcze, że
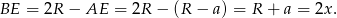
Z podobieństwa trójkątów prostokątnych 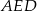 i
i 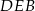 mamy
mamy
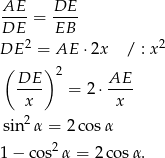
Podstawiamy teraz 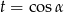 .
.
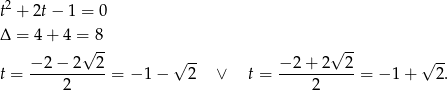
Ujemne rozwiązanie odrzucamy (bo  jest kątem ostrym) i mamy
jest kątem ostrym) i mamy 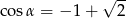 .
.
Sposób III
Podobnie jak poprzednio zauważamy, że 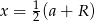 .
.
Tym razem wyliczymy 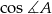 z trójkąta prostokątnego
z trójkąta prostokątnego 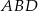 (jest on prostokątny, bo
(jest on prostokątny, bo 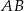 jest średnicą okręgu). Mamy
jest średnicą okręgu). Mamy
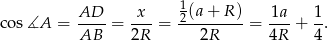
A więc tak jak w I sposobie musimy wyliczyć iloraz 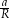 . Tym razem korzystamy z podobieństwa trójkątów
. Tym razem korzystamy z podobieństwa trójkątów 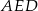 i
i 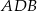 (oba są prostokątne i mają wspólny kąt).
(oba są prostokątne i mają wspólny kąt).
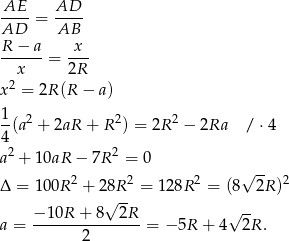
Zatem
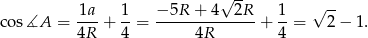
Sposób IV
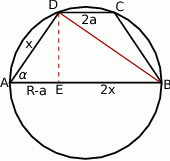
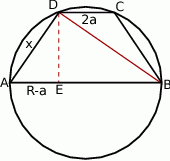
Robimy rysunek.
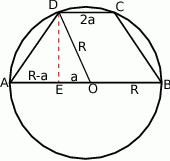
Powinno być jasne, że promień okręgu 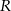 i długość krótszej podstawy
i długość krótszej podstawy 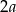 jednoznacznie wyznaczają trapez (rysujemy okrąg o promieniu
jednoznacznie wyznaczają trapez (rysujemy okrąg o promieniu 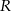 , cięciwę długości
, cięciwę długości 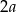 i cała reszta trapezu jest już jednoznacznie wyznaczona). Korzystając z tej obserwacji mamy plan działania: wyliczymy założenia i szukany cosinus w zależności od
i cała reszta trapezu jest już jednoznacznie wyznaczona). Korzystając z tej obserwacji mamy plan działania: wyliczymy założenia i szukany cosinus w zależności od 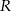 i
i  i z założeń będzie pewnie wynikać wartość cosinusa (jeżeli zadanie ma sens).
i z założeń będzie pewnie wynikać wartość cosinusa (jeżeli zadanie ma sens).
Jeżeli poprowadzimy wysokość 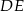 , to
, to 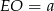 , zatem
, zatem 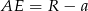 . Stosujemy twierdzenie Pitagorasa jednocześnie do trójkątów
. Stosujemy twierdzenie Pitagorasa jednocześnie do trójkątów 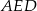 i
i 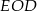 .
.
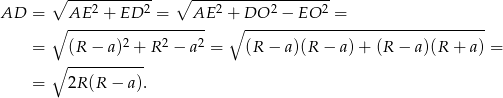
Podane założenia dają nam zatem
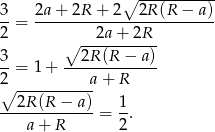
Zanim będziemy to przekształcać dalej, zobaczmy co mamy wyliczyć
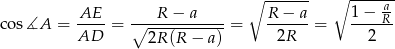
Widać więc, że tak naprawdę potrzebny nam jest iloraz 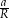 .
.
Wracamy do przekształcania założeń
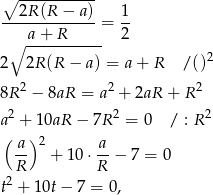
gdzie 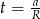 . Dalej,
. Dalej, 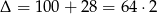 , Dodatni pierwiastek to
, Dodatni pierwiastek to 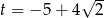 . Stąd
. Stąd
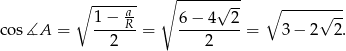
Można łatwo sprawdzić, że 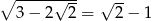 .
.
Odpowiedź: