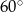/Konkursy/Zadania/Geometria/Planimetria

Zadanie nr 3334127

Dodaj do ulubionych
Dodaj do rozwiązanych

Dwusieczna kąta 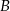B trójkąta 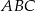ABC przecina bok 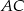AC w punkcie 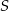S , a dwusieczna kąta 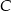C przecina bok 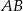AB w punkcie 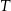T . Dwusieczne przecinają się w punkcie 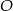O . Znajdź miarę kąta 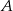A , jeżeli wiadomo, że na czworokącie 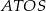ATOS można opisać okrąg.

Rozwiązanie

Zaczynamy od rysunku i oznaczmy kąty trójkąta przez 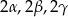2 α,2β,2γ (żeby nie mieć ułamków).

PIC

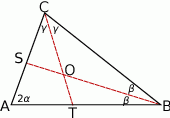
Patrząc na trójkąt 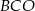BCO mamy

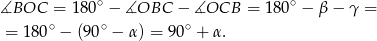
∘ ∘ ∡BOC = 180 − ∡OBC − ∡OCB = 1 80 − β− γ = = 18 0∘ − (90∘ − α) = 90∘ + α.

Po drodze skorzystaliśmy z tego, że 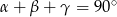α + β + γ = 90∘ .

Ponieważ na czworokącie 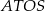ATOS można opisać okrąg, sumy miar jego przeciwległych kątów są równe 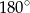∘ 180 . Zatem

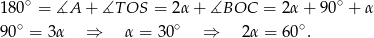
∘ ∘ 1 80 = ∡A + ∡TOS = 2α + ∡BOC = 2α + 90 + α 9 0∘ = 3α ⇒ α = 30∘ ⇒ 2 α = 60∘.

 
Odpowiedź: 60∘

Wersja PDF