Zadanie nr 6357309
Uzasadnij, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku. Jaka figurę otrzymamy, łącząc kolejno środki boków: a) rombu, b) prostokąta, c) kwadratu?
Rozwiązanie
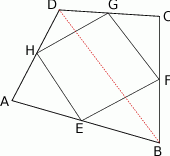
Jeżeli dorysujemy przekątną 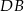 , to na mocy twierdzenia Talesa jest ona równoległa do odcinków
, to na mocy twierdzenia Talesa jest ona równoległa do odcinków 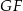 i
i 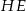 . Podobnie, odcinki
. Podobnie, odcinki 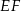 i
i 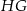 są równoległe do przekątnej
są równoległe do przekątnej 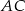 . Czworokąt
. Czworokąt 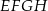 jest więc równoległobokiem.
jest więc równoległobokiem.
Jeżeli wyjściowy czworokąt jest rombem, to ponieważ przekątne rombu są prostopadłe, czworokąt 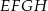 jest prostokątem. Jeżeli
jest prostokątem. Jeżeli 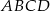 jest prostokątem, to
jest prostokątem, to 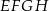 będzie rombem. W przypadku kwadratu otrzymamy kwadrat.
będzie rombem. W przypadku kwadratu otrzymamy kwadrat.
Odpowiedź: a) prostokąt, b) romb, c) kwadrat

