/Konkursy/Zadania/Geometria/Planimetria

Zadanie nr 6662989

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkącie ostrokątnym 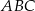ABC prawdziwa jest równość 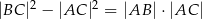2 2 |BC | − |AC | = |AB |⋅|AC | . Wykaż, że kąt 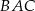BAC jest dwa razy większy od kąta ABC .

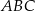Rozwiązanie

Szkicujemy trójkąt.

PIC

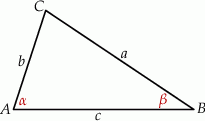
Przy oznaczeniach rysunku wiemy, że

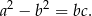
a2 − b 2 = bc.

Korzystając z twierdzenia sinusów mamy

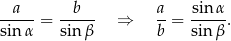
--a-- = --b-- ⇒ a-= -sin-α. sin α sin β b sin β

Teraz piszemy dwa twierdzenia cosinusów

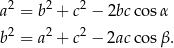
2 2 2 a = b + c − 2bcco sα b2 = a2 + c2 − 2acco sβ.

Odejmujemy te dwa równania stronami i mamy

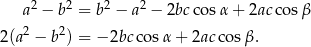
a2 − b2 = b2 − a2 − 2bc cos α+ 2acco sβ 2(a2 − b2) = − 2bcco sα + 2ac cosβ .

Podstawiamy teraz w tej równości 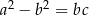a2 − b2 = bc .

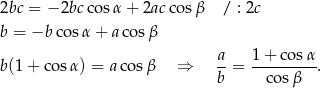
2bc = − 2bc cosα + 2ac cos β / : 2c b = −b cosα + a cosβ a 1 + co sα b(1 + cosα ) = aco sβ ⇒ --= --------- . b co sβ

Zauważmy, ze mogliśmy podzielić przez 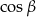cosβ , bo z założenia trójkąt 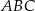ABC jest ostrokątny. Porównujemy teraz to wyrażenie z wyrażeniem otrzymanym z twierdzenia sinusów.

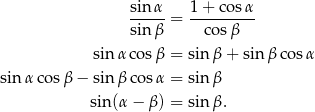
sinα- = 1-+-co-sα sinβ co sβ sinα cos β = sin β+ sin β cosα sin αco sβ − sinβ cos α = sin β sin (α− β) = sin β.

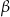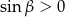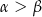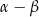Z założenia β jest kątem ostrym, więc sin β > 0 . Stąd α > β i α− β też jest kątem ostrym. Zatem

α − β = β ⇒ α = 2β.
Wersja PDF