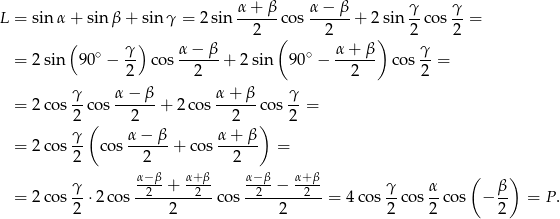Zadanie nr 6739033
Wykaż, że jeżeli 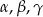 są kątami trójkąta, to
są kątami trójkąta, to
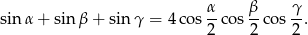
Rozwiązanie
Sposób I
Przekształcamy prawą stronę równości podstawiając 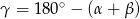
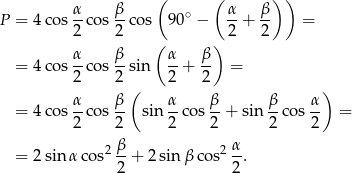
Po drodze skorzystaliśmy ze wzorów na 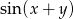 i
i 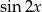 . Aby przekształcić to wyrażenie dalej, korzystamy ze wzoru:
. Aby przekształcić to wyrażenie dalej, korzystamy ze wzoru:
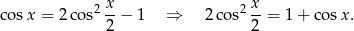
Mamy zatem
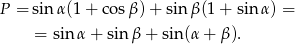
Oczywiście jest to to samo, co z lewej strony równości:
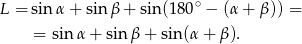
Sposób II
Tym razem skorzystamy ze wzorów na sumę sinusów i cosinusów
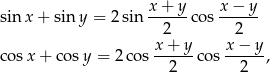
oraz ze wzoru na 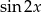 . Mamy zatem
. Mamy zatem